Question

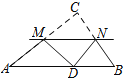
【题目】如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为__．

Answer 1

【答案】18﹣5

【解析】

作AP1⊥BD垂足为P1，当AP1旋转到与射线AD重合时（点P1与点E重合），ME就是MQ最小值；当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值，分别求出MQ的最大值与最小值即可得解.

如图作AP1⊥BD垂足为P1，∵DBA＝45°，AB＝10，∴∠P1AB＝∠DBA＝45°，AP1＝P1B＝5，∵AM＝MD＝AD＝4，当AP1旋转到与射线AD重合时（点P1与点E重合），ME就是MQ最小值＝5－4，当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值＝AM＋AF＝AM＋AB＝4＋10＝14，∴MQ的最大值与最小值的差＝14－（5－4）＝18－5，故答案为18－5.