Question

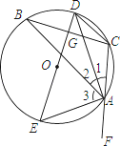
【题目】如图，已知△ABC内接于⊙O，AD、AE分别平分∠BAC和△BAC的外角∠BAF，且分别交圆于点D、F，连接DE，CD，DE与BC相交于点G．

（1）求证：DE是△ABC的外接圆的直径；

（2）设OG=3，CD=，求⊙O的半径．

Answer 1

【答案】（1）见解析 （2）5

【解析】

试题（1）根据条件AD、AE分别平分∠BAC和△BAC的外角∠BAF，证明∠2+∠3=90°即可；

（2）由∠1=∠2得出点D为弧BC的中点，从而得出DE垂直平分BC，连接BE，设圆的半径为r，然后证明△CDG∽△EBG，利用相似三角形的性质和勾股定理可求出r的值．

试题解析：（1）因为AD、AE分别是∠BAC和∠BAF的平分线

所以∠1=∠2＝∠BAC, ∠3=∠EAF＝∠BAF,

所以∠2＋∠3＝（∠BAC＋∠BAF），

因为∠BAC＋∠BAF＝180°，

所以∠2＋∠3＝90°，

所以∠EAD＝90°，

所以DE是圆O的直径；

（2）因为∠1=∠2，所以，又DE是△ABC的外接圆的直径，所以DE垂直平分BC，连接BE，则∠BEG=∠DCG，又∠BGE=∠DGC,所以△CDG∽△EBG，所以,设圆的半径为r，所以，又BG=CG，所以,在Rt△CDG中，由勾股定理可得：，解得r=5或r=-2（舍去），所以r=5．