Question

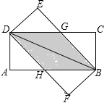
【题目】将两张完全相同的矩形纸片、按如图方式放置，为重合的对角线．重叠部分为四边形，

试判断四边形为何种特殊的四边形，并说明理由；

若，，求四边形的面积．

Answer 1

【答案】（1）四边形是菱形．（2）．

【解析】

（1）由四边形ABCD、FBED是完全相同的矩形，可得出△DAB≌△DEB（SAS），进而可得出∠ABD=∠EBD，根据矩形的性质可得AB∥CD、DF∥BE，即四边形DHBG是平行四边形，再根据平行线的性质结合∠ABD=∠EBD，即可得出∠HDB=∠HBD，由等角对等边可得出DH=BH，由此即可证出DHBG是菱形；

（2）设DH=BH=x，则AH=8-x，在Rt△ADH中，利用勾股定理即可得出关于x的一元一次方程，解之即可得出x的值，再根据菱形的面积公式即可求出菱形DHBG的面积．

解：四边形是菱形．理由如下：

∵四边形、是完全相同的矩形，

∴，，．

在和中，，

∴，

∴．

∵，，

∴四边形是平行四边形，，

∴，

∴，

∴是菱形．

由，设，则，

在中，，即，

解得：，即，

∴菱形的面积为．