题目内容
【题目】综合与探究
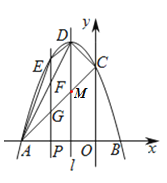
如图，已知抛物线
与
轴交于
，
两点，与
轴交于点
，对称轴为直线
，顶点为
.
(1)求抛物线的解析式及点坐标；
(2)在直线上是否存在一点
，使点到点
的距离与到点的距离之和最小？若存在，求出点的坐标；若不存在，请说明理由.
(3)在轴上取一动点
，
，过点
作轴的垂线，分别交抛物线，
，
于点
，
，
.
①判断线段
与
的数量关系，并说明理由
②连接
，
，
，当
为何值时，四边形
的面积最大？最大值为多少？
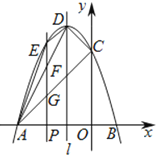
【答案】(1)
，点
坐标为
；(2)点
的坐标为
；(3)①
；②当
为-2时，四边形
的面积最大，最大值为4.
【解析】
（1）用待定系数法即可求出抛物线解析式，然后化为顶点式求出点D的坐标即可；
（2）利用轴对称-最短路径方法确定点M，然后用待定系数法求出直线AC的解析式，进而可求出点M的坐标；
（3）①先求出直线AD的解析式，表示出点F、G、P的坐标，进而表示出FG和FP的长度，然后即可判断出线段
与
的数量关系；
②根据割补法分别求出△AED和△ACD的面积，然后根据
列出二次函数解析式，利用二次函数的性质求解即可.
解：(1)由抛物线
与
轴交于
，
两点得
，
解得
，
故抛物线解析式为，
由
得点坐标为；
(2)在直线
上存在一点，到点
的距离与到点
的距离之和最小.
根据抛物线对称性
，
∴
，
∴使
的值最小的点应为直线
与对称轴
的交点，
当
时，
，
∴
，
设直线解析式为直线
，
把、分别代入得
，解之得：
，
∴直线解析式为
，
把
代入得，
，
∴
，
即当点到点
的距离与到点的距离之和最小时的坐标为；
(3)①，
理由为：
设直线
解析式为
，
把、
分别代入直线得
，解之得：
，
∴直线解析式为
，
则点
的坐标为
，
同理
的坐标为
，
则
，
，
∴
；
②∵， ，，
∴AO=3，DM=2，
∴S△ACD=S△ADM+S△CDM=
.
设点
的坐标为
，
，
∴
，
∴当为-2时，
的最大值为1.
∴
，
∴当为-2时，四边形的面积最大，最大值为4.
