题目内容

已知：如图，在平行四边形ABCD中，E、F分别是AD、BC的中点，求证：BE=DF
见解析解析:
证明：∵ 四边形ABCD是平行四边形
∴AD="BC" AD∥BC
∵E、F分别是AD、BC的中点
∴
∴DE="BF" DE∥BF
∴四边形BFDE是平行四边形
∴BE=DF
要证明BE=DF，可以证明它们所在的两个三角形全等，也可以通过证明四边形BEDF是平行四边形，再根据平行四边形的对边相等进行证明
练习册系列答案
相关题目
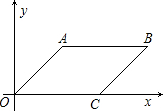精英家教网如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
5
，
5
），C（2
5
，0）．
（1）求点B的坐标．
（2）将平行四边形ABCO向左平移
5
个单位长度，求所得四边形A′B′C′O′四个顶点的坐标．
（3）求平行四边形ABCO的面积．
（1）已知：如图1，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过E点作AC的垂线，交CD的延长线于点F．求证：AB=FC．
（2）如图2，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．
（1）请直接写出点A关于y轴对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°．画出图形，直接写出点B的对应点的坐标；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
关系：①AD∥BC；②AB=CD；③∠B+∠C=180°；④∠A=∠C．
已知：在四边形ABCD中，
①
①
，
③
③
．（填序号，写出一种情况即可）  
求证：四边形ABCD是平行四边形．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3
，
3
），C（2
3
，0）．
（1）填空：点B的坐标是
（3
3
，
3
）
（3
3
，
3
）
．
（2）将平行四边形OABC向左平移
3
个单位长度，求所得四边形A′B′C′O′四个顶点的坐标．

已知：如图，在平面直角坐标系xOy中，直线AB与x轴、y轴的交点分别为A、B，OB=3，，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，

（1）求过A、B、C三点的抛物线解析式；

（2）若抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四

边形？若存在，求出点P的坐标；若不存在，说明理由；

（3）若点Q是抛物线上一个动点，使得以A、B、Q为顶点并且以AB为直角边的直角三角形，直角写出Q点坐标。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网