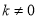题目内容
(本题满分12分)如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B、C三点的坐标;
(2)在抛物线的对称轴上找到点P,使得△PBC的周长最小,并求出点P的坐标;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G为顶点四边形是平行四边形?如果存在,请直接写出F点坐标;如果不存在,请说明理由.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一名男生投实心球,已知球行进的高度y(m)与水平距离x(m)之间的关系为
y=﹣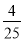 (x﹣2)2+
(x﹣2)2+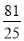 ,那么该男生此次投实心球的成绩是__.
,那么该男生此次投实心球的成绩是__.
水平距离(米) | 8.50以上 | 8.49﹣8.00 | 7.99﹣7.50 | 7.49﹣7.00 | 69.00- 6.50 | 6.49﹣6.00 | 5.9﹣5.60 | 5.5﹣5.20 | 5.1﹣4.80 | 4.79以下 |
得分 | 10分 | 9分 | 8分 | 7分 | 6分 | 5分 | 4分 | 3分 | 2分 | 1分 |


 的图象在一、三象限,则直线y=kx+k的图象经过( ).
的图象在一、三象限,则直线y=kx+k的图象经过( ). ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
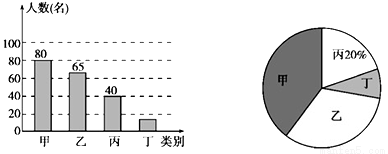
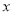 的一元二次方程
的一元二次方程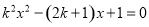 有两个不相等的实数根,那么
有两个不相等的实数根,那么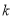 的取值范围是( )
的取值范围是( )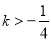 B.
B. 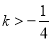 且
且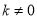 C.
C. 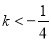 D.
D. 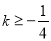 且
且