Question

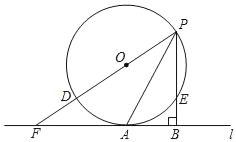
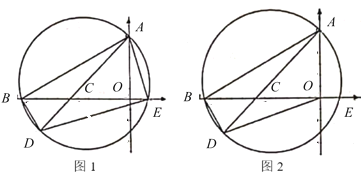
【题目】如图1，在平面直角坐标系中，已知点，的坐标分别为和，点为轴正半轴上的一个动点，过点、、作的外接圆，连结并延长交圆于点，连结、．

（1）求证：．

（2）当时，求的长度．

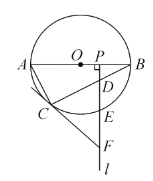
（3）如图2，连结，求线段的最小值及当最小时的外接圆圆心的坐标．

Answer 1

【答案】（1）见解析；（2）；（3）OD最小值为9，C（，）

【解析】

（1）根据圆周角定理得出∠ABD=90°，再根据同弧所对的圆周角相等得出∠ADB=∠AEB，从而证明结论；

（2）根据条件算出AB，证明△ABD∽△AOE，得出，解得AE，再根据勾股定理算出OE的长；

（3）设直线BD与y轴交于点F，得出当OD⊥BD时，OD最小，通过解直角三角形算出OD，BD，过点D作DG⊥BE于点G，设OG=x，利用勾股定理解出OG和DG，从而得到点D坐标，结合点A坐标得出圆心C的坐标.

解：（1）由题意可得：AD为⊙O的直径，

∴∠ABD=∠AOE=90°，

∵∠ADB=∠AEB，∠AOE=90°

∴∠OAE=∠BAD；

（2）∵和，

∴OA=6，OB=，

∴AB=，

∵AD=15，

由（1）得：∠OAE=∠BAD，∠ABD=∠AOE，

∴△ABD∽△AOE，

∴，

即，

解得：AE=，

∴OE=；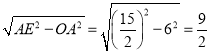

（3）设直线BD与y轴交于点F，

∵AB⊥BD，

∴∠OBD=∠OAB=90°-∠ABO，

直线AB位置不变，

∴直线BD位置不变，

∴当OD⊥BD时，OD最小，

此时，OD=OB×sin∠OBD=OB×sin∠OAB=×=×=9，

BD=，

过点D作DG⊥BE于点G，设OG=x，则BG=-x，

在△OBD中，BD2-BG2=OD2-OG2，

即，

解得：x=，即OG=，

DG=，

由题意可得点D在第三象限，

∴点D坐标为（，），而点A（0，6），

∴点C坐标为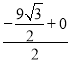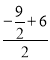（，），即（，）.