题目内容
 株洲电视塔又叫东方神龙塔,是一座钢结构带旅游的多功能综合电视塔,它是株洲市标志性景观之一.某校数学兴趣小组要测量株洲电视塔的高度,如图,他们在点C处测得电视塔的最高点A的仰角为45°,再往电视塔的方向前进125m至点D处,测得最高点A的仰角为60°.求该兴趣小组测得的株洲电视塔的高度AB.
株洲电视塔又叫东方神龙塔,是一座钢结构带旅游的多功能综合电视塔,它是株洲市标志性景观之一.某校数学兴趣小组要测量株洲电视塔的高度,如图,他们在点C处测得电视塔的最高点A的仰角为45°,再往电视塔的方向前进125m至点D处,测得最高点A的仰角为60°.求该兴趣小组测得的株洲电视塔的高度AB.
(注: ≈1.7,结果保留整数)
≈1.7,结果保留整数)
解:设株洲电视塔的高度AB为xm,
∵∠C=45°,∠B=90°,
∴∠CAB=∠C=45°,
∴BC=AB=xm,
在Rt△ABC中,tan∠ADB=tan60°= ,
,
∴BD= =
= xm,
xm,
∵CD=BC-BD,CD=125m,
∴x- x=125,
x=125,
解得:x= ≈294,
≈294,
∴株洲电视塔的高度AB为294m.
分析:首先设株洲电视塔的高度AB为xm,由题意即可求得BC=AB=xm,然后根据∠ADB的正切求得BD的长,又由CD=125m,可得方程:x- x=125,解此方程即可求得答案.
x=125,解此方程即可求得答案.
点评:本题考查仰角的知识.要求学生能借助仰角构造直角三角形并解直角三角形,注意数形结合思想与方程思想的应用.
∵∠C=45°,∠B=90°,
∴∠CAB=∠C=45°,
∴BC=AB=xm,
在Rt△ABC中,tan∠ADB=tan60°=
 ,
,∴BD=
 =
= xm,
xm,∵CD=BC-BD,CD=125m,
∴x-
 x=125,
x=125,解得:x=
 ≈294,
≈294,∴株洲电视塔的高度AB为294m.
分析:首先设株洲电视塔的高度AB为xm,由题意即可求得BC=AB=xm,然后根据∠ADB的正切求得BD的长,又由CD=125m,可得方程:x-
 x=125,解此方程即可求得答案.
x=125,解此方程即可求得答案.点评:本题考查仰角的知识.要求学生能借助仰角构造直角三角形并解直角三角形,注意数形结合思想与方程思想的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 株洲电视塔又叫东方神龙塔,是一座钢结构带旅游的多功能综合电视塔,它是株洲市标志性景观之一.某校数学兴趣小组要测量株洲电视塔的高度,如图,他们在点C处测得电视塔的最高点A的仰角为45°,再往电视塔的方向前进125m至点D处,测得最高点A的仰角为60°.求该兴趣小组测得的株洲电视塔的高度AB.
株洲电视塔又叫东方神龙塔,是一座钢结构带旅游的多功能综合电视塔,它是株洲市标志性景观之一.某校数学兴趣小组要测量株洲电视塔的高度,如图,他们在点C处测得电视塔的最高点A的仰角为45°,再往电视塔的方向前进125m至点D处,测得最高点A的仰角为60°.求该兴趣小组测得的株洲电视塔的高度AB. 小明和小刚一起去测上海东方明珠塔(BC)的高度,如图所示,他们在离塔200米的大楼楼顶A处用测角仪测得的仰角∠BAE=60°(AE与地面CD平行),塔底的俯角∠CAE=30°,则该塔的高为( )米(测角仪的高度不计)
小明和小刚一起去测上海东方明珠塔(BC)的高度,如图所示,他们在离塔200米的大楼楼顶A处用测角仪测得的仰角∠BAE=60°(AE与地面CD平行),塔底的俯角∠CAE=30°,则该塔的高为( )米(测角仪的高度不计)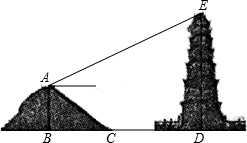 高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38,
高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38, 精确到1米)
精确到1米)