题目内容
16.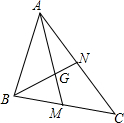 如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
如图,已知△ABC中,中线AM、BN相交于点G,如果$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.(用$\overrightarrow{a}$和$\overrightarrow{b}$表示).
分析 由△ABC中,中线AM、BN相交于点G,根据重心的性质,即可得AG=$\frac{2}{3}$AM,BG=$\frac{2}{3}$BN,继而求得$\overrightarrow{AM}$与$\overrightarrow{BG}$,然后由三角形法则求得$\overrightarrow{AB}$,$\overrightarrow{BM}$,继而求得答案.
解答 解:∵△ABC中,中线AM、BN相交于点G,
∴AG=$\frac{2}{3}$AM,BG=$\frac{2}{3}$BN,
∵$\overrightarrow{AG}$=$\overrightarrow{a}$,$\overrightarrow{BN}$=$\overrightarrow{b}$,
∴$\overrightarrow{AM}$=$\frac{3}{2}$$\overrightarrow{AG}$=$\frac{3}{2}$$\overrightarrow{a}$,$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{BN}$=$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{AB}$=$\overrightarrow{AG}$-$\overrightarrow{BG}$=$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{BM}$=$\overrightarrow{AM}$-$\overrightarrow{AB}$=$\frac{3}{2}$$\overrightarrow{a}$-($\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$)=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{BC}$=2$\overrightarrow{BM}$=$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.
故答案为:$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识.注意三角形法则的应用.

 阅读快车系列答案
阅读快车系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 2和1.6 | B. | 2和2 | C. | 2.4和1.6 | D. | 2.4和2 |
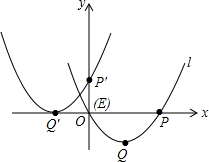 如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )
如图,将抛物线l:y=ax2-2x+a2-4(a为常数)向左并向上平移,使顶点Q的对应点Q′,抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上,则抛物线l与x轴的交点E的对应点的坐标为( )| A. | (-1,$\frac{1}{2}$) | B. | (0,0) | C. | (-$\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,0) |
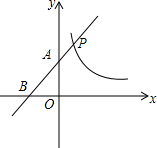 如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.
如图,直线y=x+m与双曲线y=$\frac{3}{x}$交于点P,与x轴、y轴交于B、A两点,则PA•PB=6.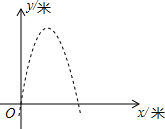 滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.
滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.
 如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为100°.
如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为100°.