题目内容
用适当的方法解方程
(1)5x(1-x)=2x-2
(2)(x-1)(x+3)=-4.
(1)5x(1-x)=2x-2
(2)(x-1)(x+3)=-4.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)首先移项,进而利用提取公因式法分解因式,进而解方程得出即可;
(2)首先去括号,进而利用完全平方公式分解因式进而解方程.
(2)首先去括号,进而利用完全平方公式分解因式进而解方程.
解答:解:(1)5x(1-x)=2x-2
5x(1-x)-2(x-1)=0,
5x(1-x)+2(1-x)=0,
(1-x)(5x+2)=0,
解得:x1=-
,x2=1;
(2)(x-1)(x+3)=-4
x2+2x-3=-4,
则x2+2x+1=0,
(x+1)2=0,
解得;x1=x2=-1.
5x(1-x)-2(x-1)=0,
5x(1-x)+2(1-x)=0,
(1-x)(5x+2)=0,
解得:x1=-
| 2 |
| 5 |
(2)(x-1)(x+3)=-4
x2+2x-3=-4,
则x2+2x+1=0,
(x+1)2=0,
解得;x1=x2=-1.
点评:此题主要考查了因式分解法解一元二次方程,正确分解因式是解题关键.

练习册系列答案
相关题目
分式方程
-
=1的解是( )
| 1 |
| x-3 |
| 2x |
| 3-x |
| A、x=-4 | ||
| B、0 | ||
C、-
| ||
D、
|
从一副扑克牌中任意抽取一张,正好为K的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知(m+2)x|m|-1+3=0为一元二次方程式,则m的值为( )
| A、2 | B、-2 |
| C、2或-2 | D、以上都不对 |
a,b,c是三个连续的正整数(a<b<c),以b为边长作正方形,分别以c,a为长和宽作长方形,那么( )
| A、长方形面积大 | B、正方形面积大 |
| C、一样大 | D、不能确定 |
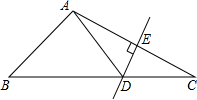 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是 二次函数y=-2x2+4x的对称轴是x=
二次函数y=-2x2+4x的对称轴是x= 在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,请你填出通过该桥洞的车高x(m)的取值范围是
在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,请你填出通过该桥洞的车高x(m)的取值范围是