题目内容
12.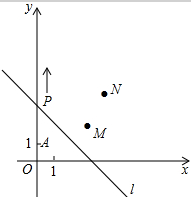 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.(1)当t=3时,求直线的解析式;
(2)当直线通过点M时,求直线l的解析式;
(3)若点M,N位于l的异侧,确定t的取值范围.
分析 (1)由t=3确定出P的坐标,代入直线l求出b的值,即可确定出直线l解析式;
(2)把M坐标代入直线l解析式求出b的值,即可确定出直线通过点M时的解析式;
(3)把N坐标代入直线l解析式求出b的值,进而求出直线l过M与N时t的值,即可确定出所求t的范围.
解答 解:(1)当t=3时,P坐标为(0,4),
把P坐标代入直线l解析式得:b=4,
则此时直线解析式为y=-x+4;
(2)把M(3,2)代入直线l解析式得:2=-3+b,即b=5,
此时直线l解析式为y=-x+5;
(3)把N(4,4)代入直线l解析式得:4=-4+b,即b=8,
此时直线l解析式为y=-x+8,
当直线l过M点时,令y=-x+5中x=0,得到y=5,即P(0,5),此时t=4;
当直线l过N点时,令y=-x+8中x=0,得到y=8,即P(0,8),此时t=7,
则点M,N位于l的异侧,t的取值范围为4<t<7.
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,待定系数法确定一次函数解析式,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
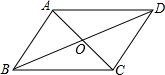 如图,在?ABCD中,对角线AC,BD相交于点O,AC+BD=36,△ABO的周长为30,求AB的长.
如图,在?ABCD中,对角线AC,BD相交于点O,AC+BD=36,△ABO的周长为30,求AB的长. 如图,将周长为10的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为14.
如图,将周长为10的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为14.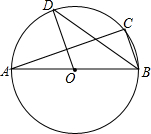 如图,AB是⊙O的直径,OB=3,BC是⊙O的弦,∠ABC的平分线交⊙O于点D,连接OD,若∠BAC=20°,则$\widehat{AD}$的长等于$\frac{7}{6}$π.
如图,AB是⊙O的直径,OB=3,BC是⊙O的弦,∠ABC的平分线交⊙O于点D,连接OD,若∠BAC=20°,则$\widehat{AD}$的长等于$\frac{7}{6}$π.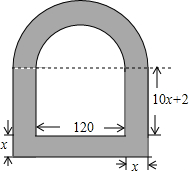 求如图所示的窗户的边框面积(上部为半圆).(单位:cm)
求如图所示的窗户的边框面积(上部为半圆).(单位:cm) 已知,在数轴上a,b,c所对应的点如图所示,化简|a|-|a+b|+|c-a|+|b-c|.
已知,在数轴上a,b,c所对应的点如图所示,化简|a|-|a+b|+|c-a|+|b-c|.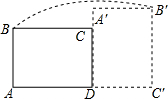 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).