题目内容
10.对于所有有理数,我们规定$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,按上述规定运算,求$|\begin{array}{l}{x+y}&{-x+y}\\{-x-y}&{x-y}\end{array}|$的值.分析 根据题意列出整式相加减的式子,再根据平方差公式进行计算即可.
解答 解:∵$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,
∴$|\begin{array}{l}{x+y}&{-x+y}\\{-x-y}&{x-y}\end{array}|$
=(x+y)(x-y)-(-x+y)(-x-y)
=x2-y2-(x2-y2)
=0.
点评 本题考查的是平方差公式,熟记平方差公式是解答此题的关键.

练习册系列答案
相关题目
20.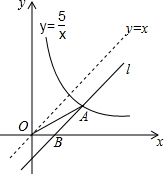 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )| A. | 5 | B. | 10 | C. | 15 | D. | 25 |
1.设a=$\sqrt{11}$+1,a在两个相邻整数之间,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
18.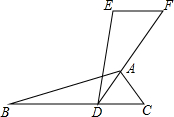 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )| A. | 50° | B. | 60° | C. | 100° | D. | 120° |

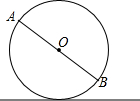 如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.
如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.