题目内容
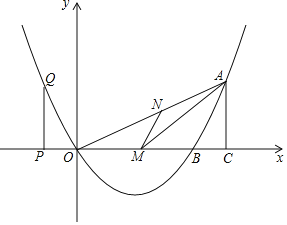
【题目】在平面直角坐标系xOy中,已知抛物线![]() .
.
(1)当m=3时,求抛物线的顶点坐标;
(2)已知点A(1,2).试说明抛物线总经过点A;
(3)已知点B(0,2),将点B向右平移3个单位长度,得到点C,若抛物线与线段BC只有一个公共点,求m的取值范围.
【答案】(1)(1,2);(2)详见解析;(3)m=3或0<m<![]() 或-3<m<0.
或-3<m<0.
【解析】
(1)把m=3代入解析式,化成顶点式,即可求得抛物线的顶点坐标;
(2)把x=1代入解析式,![]() 总等于2,与
总等于2,与![]() 无关,即可判断抛物线总经过点A(1,2);
无关,即可判断抛物线总经过点A(1,2);
(3)根据题意可以得到点C的坐标,分顶点在线段BC上、抛物线过点B(0,2)、抛物线过点C(3,2)时三种情况讨论,画出抛物线的图象,然后根据图象和题意,即可得到![]() 的取值范围.
的取值范围.
(1)把m=3代入![]() 中,得:
中,得:
![]() ,
,
∴抛物线的顶点坐标是(1,2);
(2)当x=1时,![]() ,
,
∵点A(1,2),
∴抛物线总经过点A;
(3)∵点B(0,2),由平移得C(3,2).
① 当顶点在线段BC上,抛物线与线段BC只有一个公共点.
由(1)知,抛物线的顶点A(1,2)在线段BC上,
此时,m=3;
② 当抛物线过点B(0,2)时,
将点B(0,2)代入抛物线表达式,得:
![]() ,
,
∴m=![]() >0,
>0,
此时抛物线开口向上(如图1),
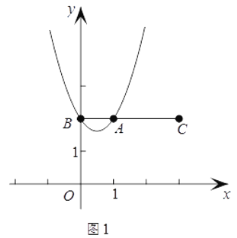
∴当0<m<![]() 时,抛物线与线段BC只有一个公共点;
时,抛物线与线段BC只有一个公共点;
③当抛物线过点C(3,2)时,
将点C(3,2)代入抛物线表达式,得:
![]() ,
,
∴![]() ,
,
此时抛物线开口向下(如图2),
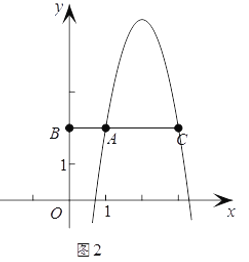
∴当![]() 时,抛物线与线段BC只有一个公共点,
时,抛物线与线段BC只有一个公共点,
综上,m的取值范围是m=3或0<m<![]() 或-3<m<0.
或-3<m<0.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除0外的全体实数,
的取值范围是除0外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 1 | 2 | 3 | 6 | … |
| … | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | … |
其中,![]() _________.
_________.
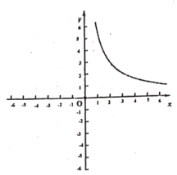
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出一条函数性质.
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________.
的实数根的情况是________.
②方程![]() 有_______个实效根;
有_______个实效根;
③关于![]() 的方程
的方程![]() 有2个实数根,
有2个实数根,![]() 的取值范围是________.
的取值范围是________.