题目内容
小丽剪了一些直角三角形纸片，她取出其中的几张进行了如下的操作：
操作一：如图，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE.
⑴如果AC=6cm,BC=8cm,试求△ACD的周长.
⑵如果∠CAD:∠BAD=4:7,求∠B的度数.
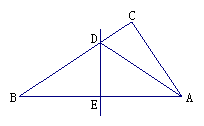
操作二：如图，小丽拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm，BC=8cm，你能求出CD的长吗？
操作三：如图，小丽又拿出另一张Rt△ABC纸片，将纸片折叠，折痕CD⊥AB。
你能证明：BC2+AD2=AC2+BD2 吗？
 |
操作一：
(1)由对称性可得AD=BD,∵△ACD的周长=AC+CD+AD ∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(㎝)
(2) 设∠CAD=4x ， ∠BAD=7x 由题意得方程：7x+7x＋4x=90 解之得 x =5
所以∠B=35
操作二：
设CD= x 则BD=8－x DE=x 由题意可得方程 
解之得 x=3 所以 CD=3㎝
操作三：
在Rt△BCD中，由勾股定理可得 
在Rt△ACD中，由勾股定理可得 AD2＋CD2= AC2
∴BC2+AD2= 
＋ AD2= AC2+BD2
练习册系列答案
相关题目
