题目内容
 已知:如图,在⊙O中,弦AB垂直平分半径ON,过点A,B的切线相交于点M,求证:△ABM是等边三角形.
已知:如图,在⊙O中,弦AB垂直平分半径ON,过点A,B的切线相交于点M,求证:△ABM是等边三角形.考点:切线的性质,等边三角形的判定,垂径定理
专题:证明题
分析:如图,作辅助线,首先证明∠MAO=∠MBO=
∠AOB;进而求出∠AOB=120°问题即可解决.
| 1 |
| 2 |
解答: 证明:如图,连接OA,OB;
证明:如图,连接OA,OB;
∵MA,MB是⊙O的切线,
∴∠MAO=∠MBO=
∠AOB;
∵弦AB垂直平分半径ON,
∴OP=
OA,∠OPA=90°,
∴∠OAP=30°,∠AOB=2∠AOP=120°,
∴∠MAO=∠MBO=
∠AOB=60°,
∴△ABM是等边三角形.
 证明:如图,连接OA,OB;
证明:如图,连接OA,OB;∵MA,MB是⊙O的切线,
∴∠MAO=∠MBO=
| 1 |
| 2 |
∵弦AB垂直平分半径ON,
∴OP=
| 1 |
| 2 |
∴∠OAP=30°,∠AOB=2∠AOP=120°,
∴∠MAO=∠MBO=
| 1 |
| 2 |
∴△ABM是等边三角形.
点评:该命题以圆为载体,以旋切角定理、垂径定理、等边三角形的判定等几何知识点的考查为核心构造而成;解题的关键是灵活运用有关定理来分析、判断.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
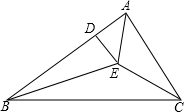 如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )
如图,E是△ABC内一点,EA、EB分别是∠BAC与∠ABC的平分线,且ED⊥AB于点D,连接EC,则∠AED+∠BEC的度数为( )| A、150° | B、165° |
| C、180° | D、195° |
 北京市汽车车牌号一般采取如图的表示方法,这种表示方法最多可以给
北京市汽车车牌号一般采取如图的表示方法,这种表示方法最多可以给
 在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?
在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长? 画出图中无盖正方体纸盒的一种表面展开图.
画出图中无盖正方体纸盒的一种表面展开图.