题目内容
如图，△ABC为⊙O的内接三角形，∠OBC=50°，则∠A等于（ ）
A．80°
B．60°
C．50°
D．40°
【答案】分析：根据等边对等角求得∠OBC的度数，再利用三角形内角和定理求得∠BOC的度数，再根据同弧所对的圆周角是该弧所对的圆心角的一半从而求得∠A的度数．
解答：解：∵OB=OC，
∴∠OBC=∠OCB=50°，
∴∠BOC=180°-2∠OBC=80°，
∴∠A=
∠BOC=40°．
故选D．
点评：本题利用了圆周角定理的三角形内角和定理求解．
解答：解：∵OB=OC，
∴∠OBC=∠OCB=50°，
∴∠BOC=180°-2∠OBC=80°，
∴∠A=
∠BOC=40°．故选D．
点评：本题利用了圆周角定理的三角形内角和定理求解．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
种不同的平行四边形，并计算其中一种平行四边形的对角线的长．
5、如图，△ABC为⊙O的内接三角形，AB是直径，∠A=20°，则∠B的度数是（ ）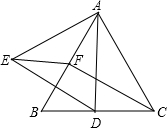
如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF，以AD为边作等边△ADE．
22、如图，△ABC为等边三角形，又DE⊥BC，EF⊥AC，FD⊥AB，垂足分别为E，F，D，则△DEF是等边三角形吗？说明你的理由．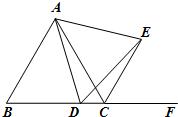
23、如图，△ABC为等边三角形，D为BC上一点，∠ADE=60°，DE交∠ACB外角平分线于E．