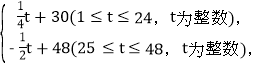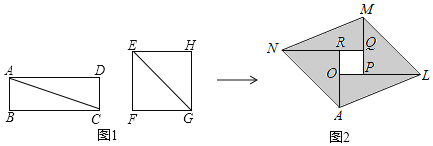题目内容
【题目】已知有理数![]() 在数轴上对应的点分别为
在数轴上对应的点分别为![]() ,其中b是最小的正整数,
,其中b是最小的正整数,![]() 满足
满足![]() .
.
(1)填空:![]() __________,
__________,![]() _____________,
_____________,![]() ___________;
___________;
(2)现将点A,点B和点C分别以每秒4个单位长度,1个单位长度和1个单位长度的速度在数轴上同时向右运动,设运动时间为t秒.
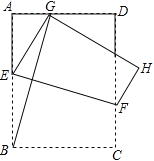
i)定义:已知![]() 为数轴上任意两点,将数轴沿线段
为数轴上任意两点,将数轴沿线段![]() 的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段
的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段![]() 的中点Q为点M和点N的折点.
的中点Q为点M和点N的折点.
试问:当t为何值时,这三个点中恰好有一点为另外两点的折点?
ii)当点A在点C左侧时(不考虑点A与点B重合),是否存在一个常数m,使得![]() 的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)-2,1,5;(2)i)当t= ![]() 或t=
或t=![]() 时,这三个点中恰好有一点为另外两点的折点;ii)存在,当常数m=2时,
时,这三个点中恰好有一点为另外两点的折点;ii)存在,当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变.
的值在一定时间范围内不随t的改变而改变.
【解析】
(1)根据b是最小的正整数得到b=1,根据![]() 求出a=-2,c=5;
求出a=-2,c=5;
(2)i)先得到运动t秒后三个点对应的数,再分三种情况分别计算t的值;
ii)先分别用t表示出AC、AB,再根据![]() 将AC、AB的式子代入即可求出常数m的值.
将AC、AB的式子代入即可求出常数m的值.
(1)∵b是最小的正整数,
∴b=1,
∵![]() ,
,
∴a+2=0,c-5=0,
∴a=-2,c=5,
故答案为:-2,1,5;
(2)
i)t秒后点A、B、C表示的数分别是:4t-2,1+t,5+t,
当点A是中点时,1+t+5+t=2(4t-2),得t= ![]() ,
,
当点B是中点时,4t-2+5+t=2(1+t),得t=![]() (舍去),
(舍去),
当点C是中点时,4t-2+1+t=2(5+t),得t=![]() ,
,
综上,当t= ![]() 或t=
或t=![]() 时,这三个点中恰好有一点为另外两点的折点;
时,这三个点中恰好有一点为另外两点的折点;
ii)存在,
∵t秒后点A、B、C表示的数分别是:4t-2,1+t,5+t,
∴AC=5+t-4t+2=7-3t,
当点A在点B的右侧时即AB =4t-2-1-t =3t-3时,
![]() =
= ![]() ,
,
∴常数m=2,此时![]() =2AC+2AB=8,即AC+AB=4,
=2AC+2AB=8,即AC+AB=4,
∵AC+AB=7-3t+3t-3=4,
∴当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变;
的值在一定时间范围内不随t的改变而改变;
当点B在点A右侧即AB=1+t-4t+2=3-3t时,
![]() =
=![]() ,
,
∴常数m=-2,此时![]() =2AC-2AB=20,即AC-AB=10,
=2AC-2AB=20,即AC-AB=10,
∵7-3t-(3-3t)=4,
∴m=-2舍去,
综上,当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变.
的值在一定时间范围内不随t的改变而改变.

 同步奥数系列答案
同步奥数系列答案【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
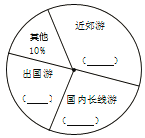
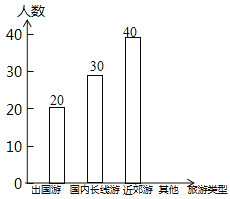
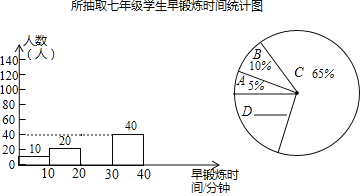
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.