题目内容
 如图,四边形ABCD、CDEF、EFGH都是正方形,则∠1+∠2=
如图,四边形ABCD、CDEF、EFGH都是正方形,则∠1+∠2=考点:相似三角形的判定与性质
专题:
分析:首先求出线段AC、AF、AG的长度(用λ表示),求出两个三角形对应边的比,进而证明△ACF∽△GCA,问题即可解决.
解答: 证明:设小正方形的边长为λ,
证明:设小正方形的边长为λ,
由勾股定理得:
AC2=λ2+λ2=2λ2,
∴AC=
λ;
同理可证:AF=
λ,AG=
λ;
∵
=
=
=
,
即
=
=
,
∴△ACF∽△GCA,
∴∠1=∠CAF;
∵∠ACB=∠CAF+∠2=45°,
∴∠1+∠2=45°.
 证明:设小正方形的边长为λ,
证明:设小正方形的边长为λ,由勾股定理得:
AC2=λ2+λ2=2λ2,
∴AC=
| 2 |
同理可证:AF=
| 5 |
| 10 |
∵
| ||
| 2λ |
| λ | ||
|
| ||
|
| ||
| 2 |
即
| AC |
| CG |
| CF |
| AC |
| AF |
| AG |
∴△ACF∽△GCA,
∴∠1=∠CAF;
∵∠ACB=∠CAF+∠2=45°,
∴∠1+∠2=45°.
点评:该题以正方形为载体,主要考查了相似三角形的判定及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
在数轴上与-3距离4个单位的点表示的数是( )
| A、-1 | B、-1和7 |
| C、1 | D、1和-7 |
若a2-1=b,则代数式-2a2-2+2b的值为( )
| A、4 | B、0 | C、-4 | D、-2 |
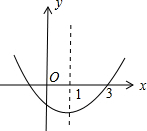 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),下列结论中,正确的是 如图,△ABC中,∠C=90°,AB=10,AD平分∠BAC,若CD=3,则△ABD的面积为
如图,△ABC中,∠C=90°,AB=10,AD平分∠BAC,若CD=3,则△ABD的面积为