Question

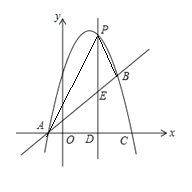
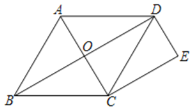
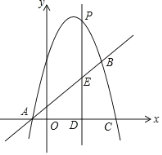
【题目】如图，抛物线与直线相交于，两点,且抛物线经过点

（1）求抛物线的解析式；

（2）点P是抛物线上的一个动点(不与点A. 点B重合)，过点P作直线PD⊥x轴于点D，交直线AB于点E.当PE=2ED时，求P点坐标；

（3）点P是直线上方的抛物线上的一个动点，求的面积最大时的P点坐标.

Answer 1

【答案】（1）y=x2＋4x＋5（2）P点坐标为（2，9）或（6，7）；（3）P（，）.

【解析】

（1）先由点B在直线y＝x＋1上求出点B的坐标，再利用待定系数法求解可得；

（2）可设出P点坐标，则可表示出E、D的坐标，从而可表示出PE和ED的长，由条件可知到关于P点坐标的方程，则可求得P点坐标；

（3）连接AP,BP，根据S= S+ S=，根据二次函数性质得到最大值，即可求出P点坐标.

解：（1）∵点B（4，m）在直线y＝x＋1上，

∴m＝4＋1＝5，

∴B（4，5），

把A、B、C三点坐标代入抛物线解析式可得

，

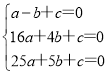解得

，

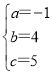∴抛物线解析式为y＝x2＋4x＋5；

（2）设P（x，x2＋4x＋5），则E（x，x＋1），D（x，0），

则PE＝|x2＋4x＋5（x＋1）|＝|x2＋3x＋4|，DE＝|x＋1|，

∵PE＝2ED，

∴|x2＋3x＋4|＝2|x＋1|，

当x2＋3x＋4＝2（x＋1）时，解得x＝1或x＝2，但当x＝1时，P与A重合不合题意，舍去，

∴P（2，9）；

当x2＋3x＋4＝2（x＋1）时，解得x＝1或x＝6，但当x＝1时，P与A重合不合题意，舍去，

∴P（6，7）；

综上可知P点坐标为（2，9）或（6，7）；

（3）∵点P是直线上方的抛物线上的一个动点，

设（x，x2＋4x＋5），则E（x，x＋1），D（x，0），

则PE＝x2＋4x＋5（x＋1）＝x2＋3x＋4，

∴= S+ S==

=

∴当x=，的面积最大

把x=代入y＝x2＋4x＋5，解得y=

故P（，）.