题目内容
设x，y为正整数，并计算它们的倒数和；接着将这两个正整数x，y分别加上1、2后，再计算它们的倒数和，请问经过这样操作之后，倒数和之差的最大值是________．
分析：列出算式，再分别通分得出
+
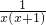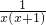，根据x，y为正整数得出x（x+1）和y（y+2）也是正整数，求出要使+最大，必须x y取最小的数，即x=y=1，代入求出即可．解答：（
+
）-（
+
）=
-+-=
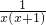+，∵x，y为正整数，
∴x（x+1）和y（y+2）也是正整数，
∵要使
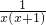+最大，必须x y取最小的数，
当x=y=1时，最大值是：
+
=．故答案为：
．点评：本题考查了分式的混合运算，解此题的关键是求出x y的值，本题比较好，但有一定的难度．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
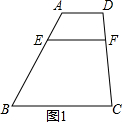如图1，梯形ABCD中，AD∥BC，BC=a，AD=b，点E、F分别是两腰AB、CD上的点，且EF∥AD，设AE=d1、BE=d2，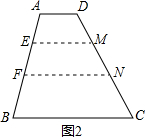
时，有EF=
；
时，有EF=
；
时，有EF=
；
时，有EF=
；当
时，有EF=
；
时，有
．
时，有EF=______；当
时，EF=______．
时，分别能得到什么结论（其中m、n均为正整数）并证明你的结论；
时，有何结论（其中m、n均为正整数）写出你的结论．
