题目内容
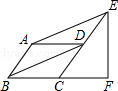
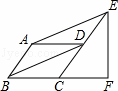
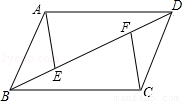
如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=![]() ,则AB的长是 1 .
,则AB的长是 1 .
考点:
平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
分析:
根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.
解答:
解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=![]() ,
,
∴CE=2,
∴AB=1,
故答案为1.
点评:
本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目

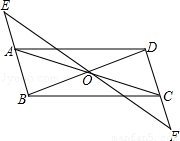
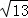 .
.
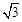 ,则AB的长是
.
,则AB的长是
.