题目内容
如图5219,AB,CD是⊙O的直径,点E在AB的延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD的延长线于点G,DG=GE=3,连接FD.
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
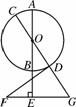
(1)解:设⊙O的半径为r.
∵BE=2,DG=3,∴OE=2+r,OG=3+r.
∵EF⊥AB,∴∠AEG=90°.
在Rt△OEG中,根据勾股定理,得OE2+EG2=OG2,
∴(2+r)2+32=(3+r)2,解得r=2.
(2)证明:∵EF=2,EG=3,∴FG=EF+EG=3+2=5.
∵DG=3,OD=2,
∴OG=DG+OD=3+2=5.∴FG=OG.
∵DG=EG,∠G=∠G,∴△DFG≌△EOG.
∴∠FDG=∠OEG=90°.∴DF⊥OD.
∴DF是⊙O的切线.

练习册系列答案
相关题目
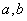 ,即
,即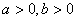 ,有下面的不等式:
,有下面的不等式: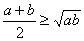 当且仅当
当且仅当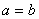 时取到等号
时取到等号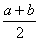 叫做正数
叫做正数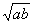 叫做正数
叫做正数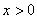 ,求函数
,求函数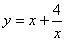 的最小值。
的最小值。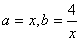 ,则有
,则有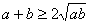 ,得
,得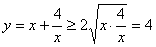 ,当且仅当
,当且仅当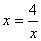 时,即
时,即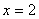 时,函数有最小值,最小值为
时,函数有最小值,最小值为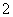 。
。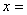 时,函数
时,函数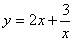 取到最小值,最小值
取到最小值,最小值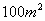 的矩形花园,问这个矩形的长、宽各为多
的矩形花园,问这个矩形的长、宽各为多 少时,所
少时,所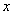 取何值时,函数
取何值时,函数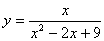 取到最大值,最大值为多少?
取到最大值,最大值为多少?
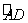 =
= C.∠ADB=∠ACB D.∠DAB=∠CBA
C.∠ADB=∠ACB D.∠DAB=∠CBA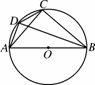

 r B.
r B. r C.r D.2r
r C.r D.2r