题目内容
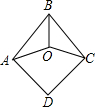 如图,O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO=________.
如图,O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO=________.
150°
分析:由OA=OB=OC,可得A,B,C在以O为圆心,OA为半径的圆上,由圆周角定理可求得∠AOC的度数,然后由四边形的内角和定理,求得答案.
解答:∵OA=OB=OC,
∴A,B,C在以O为圆心,OA为半径的圆上,
∴∠AOC=2∠ABC=140°,
∵∠ADC=70°,
∴∠DAO+∠DCO=360°-∠AOC-∠ADC=150°.
故答案为:150°.
点评:此题考查了圆周角定理以及四边形的性质.此题难度适中,注意掌握数形结合思想的应用.
分析:由OA=OB=OC,可得A,B,C在以O为圆心,OA为半径的圆上,由圆周角定理可求得∠AOC的度数,然后由四边形的内角和定理,求得答案.
解答:∵OA=OB=OC,
∴A,B,C在以O为圆心,OA为半径的圆上,
∴∠AOC=2∠ABC=140°,
∵∠ADC=70°,
∴∠DAO+∠DCO=360°-∠AOC-∠ADC=150°.
故答案为:150°.
点评:此题考查了圆周角定理以及四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
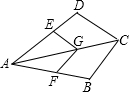
 10、如图,L是四边形ABCD的对称轴,如果AD∥BC,则有以下结论:
10、如图,L是四边形ABCD的对称轴,如果AD∥BC,则有以下结论: 7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( )
7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( ) 如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的是( )
如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的是( ) 如图,CD是线段AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是
如图,CD是线段AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是