题目内容
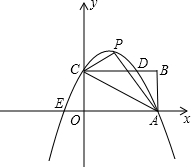
 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数 (x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为 .
(x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为 .
【答案】分析:根据反比例函数图象上的点E、F、D入手,分别找出△OCF、△OAE、矩形OABC的面积与|k|的关系,列出等式求出k值.
解答: 解:连接OF,EO,
解:连接OF,EO,
∵点D为对角线OB的中点,四边形BEDF的面积为1,
∴S△BDF=S△ODF,S△BDE=S△ODE,
∴四边形FOED的面积为1,
由题意得:E、M、D位于反比例函数图象上,则S△OCF= ,S△OAE=
,S△OAE= ,
,
过点D作DG⊥y轴于点G,作DN⊥x轴于点N,则S□ONDG=k,
又∵D为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONDG=4k,
由于函数图象在第一象限,k>0,则 +
+ +2=4k,
+2=4k,
解得:k= .
.
故答案为: .
.
点评:本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于k.本知识点是中考的重要考点,同学们应高度关注.
解答:
 解:连接OF,EO,
解:连接OF,EO,∵点D为对角线OB的中点,四边形BEDF的面积为1,
∴S△BDF=S△ODF,S△BDE=S△ODE,
∴四边形FOED的面积为1,
由题意得:E、M、D位于反比例函数图象上,则S△OCF=
 ,S△OAE=
,S△OAE= ,
,过点D作DG⊥y轴于点G,作DN⊥x轴于点N,则S□ONDG=k,
又∵D为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONDG=4k,
由于函数图象在第一象限,k>0,则
 +
+ +2=4k,
+2=4k,解得:k=
 .
.故答案为:
 .
.点评:本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于k.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是