题目内容
15.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分:A.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点,若四边形EFGH的面积12,则四边形ABCD的面积为24.
B.如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是16.1m.(精确到0.1m)

分析 A、由中位线性质得GH∥BD,则△CHG∽△BDC,可得面积比为1:4,同理得S△AEF=$\frac{1}{4}$S△ADB,则S△CHG+S△AEF=$\frac{1}{4}$S四边形ABCD,有S△CHG+S△AEF+S△DEH+S△BFG=$\frac{1}{2}$S四边形ABCD,四边形EFGH的面积等于四边形ABCD面积的一半,代入得出结论.
B、作辅助线,构建直角三角形,先求AH的长,再求BH的长,即CG的长,也就是影子的长.
解答 解:A、∵点E、F、G、H分别为边AD、AB、BC、CD的中点,
∴HG是△DBC的中位线,
∴GH∥BD,
∴△CHG∽△BDC,
∴S△CHG=$\frac{1}{4}$S△BDC,
同理S△AEF=$\frac{1}{4}$S△ADB,
∴S△CHG+S△AEF=$\frac{1}{4}$S△BDC+$\frac{1}{4}$S△ADB=$\frac{1}{4}$S四边形ABCD,
同理S△DEH+S△BFG=$\frac{1}{4}$S四边形ABCD,
∴S△CHG+S△AEF+S△DEH+S△BFG,
=$\frac{1}{4}$S四边形ABCD+$\frac{1}{4}$S四边形ABCD,
=$\frac{1}{2}$S四边形ABCD,
∴S四边形ABCD=2S四边形EFGH=2×12=24;
故答案为:24.
B、延长EA交CD于G,过G作GH⊥AB于H,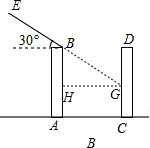
∵太阳光与水平线的夹角为30°,
∴∠AGH=30°,
∵BC=GH=24,
在Rt△AHG中,tan30°=$\frac{AH}{HG}$,
∴AH=24×tan30°=24×$\frac{\sqrt{3}}{3}$=8$\sqrt{3}$,
∴CG=BH=AB-BH=30-8$\sqrt{3}$=30-8×1.732≈16.1,
故答案为:16.1.
点评 A题考查了中点四边形,利用三角形中位线的性质可得边平行和大小关系,也可以得面积的比,由此可知中点四边形的面积等于原四边形面积的一半;B题考查了平行投影,首先要明确太阳光线是平行光线,通过构建直角三角形,利用三角函数求边长.

| A. | 1-3 | B. | -22 | C. | -4×0 | D. | |-5| |
 如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )| A. | 74° | B. | 63° | C. | 64° | D. | 73° |
| A型客车 | B型客车 | |
| 载客量(人/辆) | 45 | 28 |
| 租金(元/辆) | 400 | 250 |
(1)用含x的代数式填写下表:
| 车辆数(辆) | 载客量(人) | 租金(元) | |
| A型客车 | x | 45x | 400x |
| B型客车 | 13-x | 28(13-x) | 250(13-x) |
 a、b、c在数轴上的对应点如图所示,化简|a-b|+|b-c|-|c-a|=0.
a、b、c在数轴上的对应点如图所示,化简|a-b|+|b-c|-|c-a|=0. 如图,点A是x轴正半轴上的任意一点,过点A作EF∥y轴,分别交反比例函数y1=$\frac{{k}_{{\;}_{1}}}{x}$(y1>0)和y2=$\frac{{k}_{2}}{x}$(y2<0)的图象于点E、F,且$\frac{EA}{FA}$=$\frac{5}{3}$,连接OE、OF,有下列结论:①这两个函数的图象关于x轴对称;②△EOF的面积为$\frac{1}{2}$(k1-k2);③$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{3}{5}$;④当∠EOF=90°时,$\frac{OE}{OF}$=$\frac{\sqrt{15}}{3}$,其中正确的是( )
如图,点A是x轴正半轴上的任意一点,过点A作EF∥y轴,分别交反比例函数y1=$\frac{{k}_{{\;}_{1}}}{x}$(y1>0)和y2=$\frac{{k}_{2}}{x}$(y2<0)的图象于点E、F,且$\frac{EA}{FA}$=$\frac{5}{3}$,连接OE、OF,有下列结论:①这两个函数的图象关于x轴对称;②△EOF的面积为$\frac{1}{2}$(k1-k2);③$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{3}{5}$;④当∠EOF=90°时,$\frac{OE}{OF}$=$\frac{\sqrt{15}}{3}$,其中正确的是( ) 如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点.
如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点. 如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.