题目内容
已知等腰△ABC的腰AB=AC=10,BC=12,若以BC为中点为圆心做圆,当半径r满足什么条件,该圆与两腰所在直线
(1)相离?
(2)相切?
(3)相交?
(1)相离?
(2)相切?
(3)相交?
考点:直线与圆的位置关系
专题:计算题
分析:过BC的中点0作OD⊥AB于D,OE⊥AC于E,连接AO,如图,根据等腰三角形的性质得AO⊥BC,AO平分∠BAC,在Rt△AOB中利用勾股定理计算出AO=8,再利用面积法计算出OD=
,再根据角平分线的性质得OE=OD=
,然后根据直线和圆的位置关系的判定方法求解.
| 24 |
| 5 |
| 24 |
| 5 |
解答:解: 过BC的中点0作OD⊥AB于D,OE⊥AC于E,连接AO,如图,
过BC的中点0作OD⊥AB于D,OE⊥AC于E,连接AO,如图,
∵AB=AC,点O为BC的中点,
∴AO⊥BC,AO平分∠BAC,
在Rt△AOB中,∵AB=10,OB=
BC=6,
∴AO=
=8,
∵
•OD•AB=
AO•OB,
∴OD=
=
,
而AO为∠BAC的平分线,
∴OE=OD=
,
(1)当0<r<
时,该圆与两腰所在直线相离;
(2)当r=
时,该圆与两腰所在直线相切;
(3)当r>
时,该圆与两腰所在直线相交.
 过BC的中点0作OD⊥AB于D,OE⊥AC于E,连接AO,如图,
过BC的中点0作OD⊥AB于D,OE⊥AC于E,连接AO,如图,∵AB=AC,点O为BC的中点,
∴AO⊥BC,AO平分∠BAC,
在Rt△AOB中,∵AB=10,OB=
| 1 |
| 2 |
∴AO=
| AB2-OB2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=
| 6×8 |
| 10 |
| 24 |
| 5 |
而AO为∠BAC的平分线,
∴OE=OD=
| 24 |
| 5 |
(1)当0<r<
| 24 |
| 5 |
(2)当r=
| 24 |
| 5 |
(3)当r>
| 24 |
| 5 |
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,若直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了等腰三角形的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
在下列代数式中:-
,
ab,-n,1,
,单项式的个数有( )
| x |
| 2 |
| 2 |
| 2 |
| x |
| A、2个 | B、3个 | C、4个 | D、5个 |
下面各点中,在直线y=-2x上的是( )
| A、(2,1) |
| B、(-1,2) |
| C、(1,2) |
| D、(-2,-1) |
小明在拼图时发现8个一样大小的长方形恰好拼成一个大的长方形,如图1所示.小红看见了,说:“我也来试一试.“结果小红七拼八凑,拼成如图2那样的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形,则每个小长方形的长和宽分别为( )


| A、10mm,18mm |
| B、18mm,10mm |
| C、10mm,6mm |
| D、6mm,10mm |
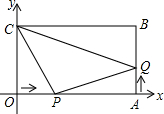 如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以 在山坡上种树,要求相邻两棵树之间的水平距离是3.5m,测得斜坡上相邻两树之间的坡面距离为5m,试求斜坡的倾斜角α的度数(精确到1°)
在山坡上种树,要求相邻两棵树之间的水平距离是3.5m,测得斜坡上相邻两树之间的坡面距离为5m,试求斜坡的倾斜角α的度数(精确到1°)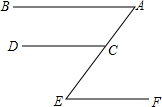 如图,CD∥EF,∠ECD=∠A,则EF∥AB,说明理由如下:
如图,CD∥EF,∠ECD=∠A,则EF∥AB,说明理由如下: