题目内容
14.在△ABC中,AB=AC=8,作AB边的垂直平分线交AB边于点D,交直线AC于点E,若DE=3,则线段CE的长为3或13.分析 分直线DE与线段AC交于E和直线DE与线段CA的延长线交于E两种情况,根据线段的垂直平分线的性质解答即可.
解答 解: 如图1,当直线DE与线段AC交于E时,连接EB,
如图1,当直线DE与线段AC交于E时,连接EB,
∵DE是AB边的垂直平分线,
∴∠ADE=90°,AD=$\frac{1}{2}$AB=4,又DE=3,
由勾股定理得,AE=5,
则CE=AC-AE=3;
如图2,当直线DE与线段CA的延长线交于E时,连接EB, ∵DE是AB边的垂直平分线,
∵DE是AB边的垂直平分线,
∴∠ADE=90°,AD=$\frac{1}{2}$AB=4,又DE=3,
由勾股定理得,AE=5,
则CE=AC+AE=13,
故答案为:3或13.
点评 本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.用形状相同的两种菱形拼成如图所示的图案,用an表示第n个菱形的个数,则an(用含n的式子表示)为( )


| A. | 5n-1 | B. | 8n-4 | C. | 6n-2 | D. | 4n+4 |
6.高安市出租车司机小李某天营运全是在东西走向的320国道上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如表:
(1)将最后一名乘客送达目的地时,小李距下午出发地点的距离是多少千米?
(2)若汽车耗油量a升/千米,这天下午汽车耗油共多少升?
| +15 | -3 | +14 | -11 | +10 | -12 |
(2)若汽车耗油量a升/千米,这天下午汽车耗油共多少升?
 如图,已知DE⊥DB于D,∠ADE=56°,DC是∠ADB的平分线,则∠ADC=17°.
如图,已知DE⊥DB于D,∠ADE=56°,DC是∠ADB的平分线,则∠ADC=17°.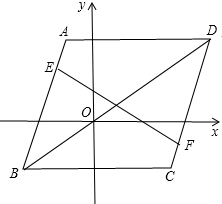 如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).
如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).