Question

如图，凸八边形A_lA₂A₃A₄A₅A₆A₇A₈中，∠A_l=∠A₅，∠A₂=∠A₆，∠A₃=∠A₇，∠A₄=∠A₈，试证明：该凸八边形内任意一点到8条边的距离之和是一个定值．

Answer 1

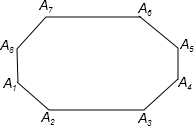
证明：延长A₈A₁，A₃A₂相交于点M，延长A₂A₃，A₅A₄相交于点N，延长A₄A₅，A₇A₆相交于点P，延长A₆A₇，A₁A₈相交于点Q，如图，
由∠A₁=∠A₅，∠A₂=∠A₆，得∠MA₁A₂=∠PA₅A₆，∠MA₂A₁=∠PA₆A₅，有∠M=∠P，
同理可证∠N=∠Q，
∴MNPQ为平行四边形，
即A₁A₈∥A₄A₅，A₂A₃∥A₇A₈，
同理可证A₁A₂∥A₅A₆，A₃A₄∥A₇A₈，
∴八边形内任意一点到A₂A₃和A₇A₈的距离和为平行线A₂A₃和A₇A₈间的距离，是一个定值．
可以推得凸八边形内任意一点到8条边的距离之和是一个定值．
分析：将八边形问题转化为熟悉的图形来解决，想象完整四边形截去4个角就得到八边形，就可知向外作辅助线，关键是证明对边平行．
点评：本题重在考查平行四边形的性质，即能够判定四边形MNPQ为平行四边形为此题的解题关键．