题目内容
 已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于
已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于
- A.90°
- B.60°
- C.45°
- D.30°
C
分析:先连接AC,由于圆的内接正方形将圆分成四等分,所以∠ACD=45°,由于∠ABP、∠ACP对着同一条弧,由圆周角定理知∠ACP=∠ABP,即∠ABP+∠PCD=∠ACD=45°,由此得解.
解答: 解:连接AC,
解:连接AC,
∵四边形ABCD是圆的内接正方形,
∴∠ACD=45°;
而∠ABP=∠ACP,则∠ABP+∠DCP=∠ACD=45°,
故选C.
点评:此题主要考查的是圆内接正多边形的性质以及圆周角定理的应用,难度不大,解题的关键是根据圆周角定理得出∠ABP+∠PCD=∠ACD.
分析:先连接AC,由于圆的内接正方形将圆分成四等分,所以∠ACD=45°,由于∠ABP、∠ACP对着同一条弧,由圆周角定理知∠ACP=∠ABP,即∠ABP+∠PCD=∠ACD=45°,由此得解.
解答:
 解:连接AC,
解:连接AC,∵四边形ABCD是圆的内接正方形,
∴∠ACD=45°;
而∠ABP=∠ACP,则∠ABP+∠DCP=∠ACD=45°,
故选C.
点评:此题主要考查的是圆内接正多边形的性质以及圆周角定理的应用,难度不大,解题的关键是根据圆周角定理得出∠ABP+∠PCD=∠ACD.

练习册系列答案
相关题目
已知正方形内接于半径是10,圆心角为90°的扇形(即正方形的各顶点都在扇形上),则正方形的边长是( )
A、5
| ||||
B、2
| ||||
C、2
| ||||
D、5
|
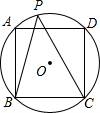 已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP=
已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP= 已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于( )
已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于( )