题目内容
4.当x>-2时,$\frac{1}{{\sqrt{x+2}}}$有意义.分析 根据二次根式有意义和分母不为0,即可解答.
解答 解:根据题意得:x+2>0,
解得:x>-2,
故答案为:x>-2.
点评 本题考查了二次根式有意义的条件,解决本题的关键是二次根式,被开方数非负,但是在分母上,分母不能为0.

练习册系列答案
相关题目
12.已知α为锐角,则m=sin2α+cos2α的值( )
| A. | m>1 | B. | m=1 | C. | m<1 | D. | m≥1 |
19.下列计算正确的是( )
| A. | $\sqrt{13}+\sqrt{3}=\sqrt{16}=4$ | B. | $\sqrt{121÷4}=\sqrt{121}÷\sqrt{4}=\frac{11}{2}$ | C. | $3+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{4\frac{1}{3}}=2\sqrt{\frac{1}{3}}$ |
14.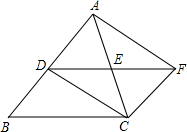 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
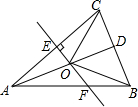 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )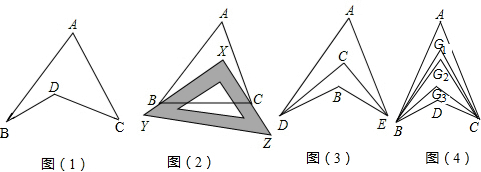
 如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以
如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以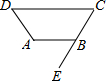 如图,AB∥CD,∠ABE=50°,∠D=∠C,则∠D=50°.
如图,AB∥CD,∠ABE=50°,∠D=∠C,则∠D=50°.