题目内容
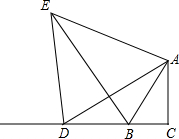 如图,Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=α,且∠AED=∠ADE=α.
如图,Rt△ABC中,D是CB延长线上一点,以AD为边作△ADE,连接BE,∠ABC=α,且∠AED=∠ADE=α.(1)在图中作出△ABC关于直线AC的轴对称图形;
(2)试判断BE,DC与BC的数量关系,并证明你的结论.
考点:作图-轴对称变换,全等三角形的判定与性质
专题:
分析:(1)利用轴对称图形的性质得出对应点B′的位置进而得出答案;
(2)利用轴对称图形的性质结合全等三角形的判定方法得出即可.
(2)利用轴对称图形的性质结合全等三角形的判定方法得出即可.
解答: 解:(1)如图所示:作B关于AC的对称点B′;
解:(1)如图所示:作B关于AC的对称点B′;
(2)BE-DC=BC,
证明:∵AB=AB′,∠ABC=α,
∴∠AB′B=α,
∵∠ABC=α,且∠AED=∠ADE=α,
∴AE=AD,∠BAB′=∠DAE=180°-2α,
∴∠EAB=∠DAB′,
在△AEB和△AD B′中,
,
∴△AEB≌△AD B′(SAS),
∴BE=B′D,
∴BE-DC=BC.
 解:(1)如图所示:作B关于AC的对称点B′;
解:(1)如图所示:作B关于AC的对称点B′;(2)BE-DC=BC,
证明:∵AB=AB′,∠ABC=α,
∴∠AB′B=α,
∵∠ABC=α,且∠AED=∠ADE=α,
∴AE=AD,∠BAB′=∠DAE=180°-2α,
∴∠EAB=∠DAB′,
在△AEB和△AD B′中,
|
∴△AEB≌△AD B′(SAS),
∴BE=B′D,
∴BE-DC=BC.
点评:此题主要考查了轴对称变换以及全等三角形的判定与性质,得出△AEB≌△AD B′是解题关键.

练习册系列答案
相关题目
 学校要把校园内一块长20米,宽12米的长方形空地进行绿化,计划中间种花,四周留出宽度相同的地种草坪,且花坛面积为180平方米,求草坪的宽度.
学校要把校园内一块长20米,宽12米的长方形空地进行绿化,计划中间种花,四周留出宽度相同的地种草坪,且花坛面积为180平方米,求草坪的宽度. 在直角坐标系内的位置如图所示:
在直角坐标系内的位置如图所示: 如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为
如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为 已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.