Question

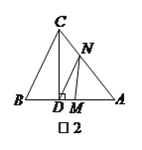
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D，E分别在AB，AC上，CE＝BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF.

(1)补充完成图形；

(2)若EF∥CD，求证：∠BDC＝90°.

Answer 1

【答案】见解析

【解析】试题分析：（1）根据题意补全图形，如图所示；
（2）由旋转的性质得到为直角，由EF与CD平行，得到为直角，利用SAS得到与全等，利用全等三角形对应角相等即可得证．

试题解析：(1)补全图形，如图所示；

(2)由旋转的性质得：

∴∠DCE+∠ECF=，

∵∠ACB=，

∴∠DCE+∠BCD=，

∴∠ECF=∠BCD，

∵EF∥DC，

∴∠EFC+∠DCF=，

∴∠EFC=，

在△BDC和△EFC中，

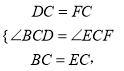
∴△BDC≌△EFC(SAS)，

∴∠BDC=∠EFC=.