题目内容
1.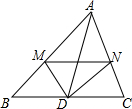 在任意△ABC中,D为BC中点,DM平分∠ADB交AB于点M,DN平分∠ADC交AC于点N,连接MN,如图所示,则MN与BM+CN的关系为( )
在任意△ABC中,D为BC中点,DM平分∠ADB交AB于点M,DN平分∠ADC交AC于点N,连接MN,如图所示,则MN与BM+CN的关系为( )| A. | BM+CN>MN | B. | BM+CN<MN | C. | BM+CN=MN | D. | 无法确定 |
分析 在AD上取DH=BD=DC,再利用全等三角形的判定和性质得出MH=BM,NH=CN,利用三角形三边关系解答即可.
解答 解:在AD上取DH=BD=DC,
∵DM平分∠ADB交AB于点M,DN平分∠ADC交AC于点N,
∴∠BDM=∠HDM,∠CDN=∠HDN,
在△BDM与△HDM中,
$\left\{\begin{array}{l}{BD=DH}\\{∠BDM=∠HDM}\\{DM=DM}\end{array}\right.$,
∴△BDM≌△HDM(SAS),
∴BM=MH,
同理可得:HN=CN,
∵MH+HN=BM+CN>MN,
故选A
点评 此题考查全等三角形的判定和性质,关键是利用全等三角形的判定和性质得出MH=BM,NH=CN.

练习册系列答案
相关题目
6.我们把5个一元硬币摞在一起测得高度大约为1cm,那么10万个这样的硬币摞在一起,其高度最接近于( )
| A. | 地球赤道的长度 | B. | 地球半径的长度 | ||
| C. | 70层大厦的高度 | D. | 学校操场国旗旗杆的高度 |
10.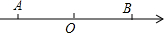 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )| A. | 2 | B. | x+5 | C. | -2 | D. | 4 |
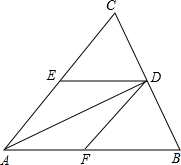 如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.
如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.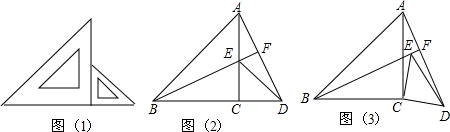
 如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.
如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.