题目内容
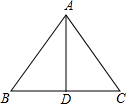 如图所示,等腰三角形△ABC中,AB=AC=5,BC=6,线段AD⊥BC于点D.
如图所示,等腰三角形△ABC中,AB=AC=5,BC=6,线段AD⊥BC于点D.(1)求等腰三角形△ABC的面积;
(2)建立适当的直角坐标系,使其中一个顶点的坐标是(-2,0),并写出其余两顶点的坐标.
解:
考点:等腰三角形的性质,坐标与图形性质,勾股定理
专题:
分析:(1)由条件可知BD=CD,在Rt△ABD中可求得AD,则可求得△ABC的面积;
(2)以BC所在直线为x轴,BC的靠近B的三等分点为坐标原点,则B点坐标为(-2,0),再结合线段的长度可求得A、C的坐标.
(2)以BC所在直线为x轴,BC的靠近B的三等分点为坐标原点,则B点坐标为(-2,0),再结合线段的长度可求得A、C的坐标.
解答: 解:
解:
(1)∵AB=AC=5,AD⊥BC,
∴BD=CD=
BC=3,
在Rt△ABD中,由勾股定理可求得AD=4,
∴S△ABC=
BC•AD=
×6×4=12;
(2)如图,以BC所在直线为x轴,BC的靠近B的三等分点为坐标原点,可知B点坐标为(-2,0),
则CO=4,DO=1,且AD=4,
∴C为(4,0),A为(1,4).
 解:
解:(1)∵AB=AC=5,AD⊥BC,
∴BD=CD=
| 1 |
| 2 |
在Rt△ABD中,由勾股定理可求得AD=4,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图,以BC所在直线为x轴,BC的靠近B的三等分点为坐标原点,可知B点坐标为(-2,0),
则CO=4,DO=1,且AD=4,
∴C为(4,0),A为(1,4).
点评:本题主要考查等腰三角形的性质,掌握等腰三角形底边上的高、中线和顶角的角平分线是解题的关键.

练习册系列答案
相关题目
下列计算中,正确的是( )
| A、a2•a3=a6 |
| B、a6÷a2=a3 |
| C、(2a2b)2=2a4b2 |
| D、(a3b)2=a6b2 |
 在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.
在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.