题目内容
推理运算
已知点P是函数y=
x(x>0)图象上一点,PA⊥x轴于点A,交函数y=
(x>0)图象于点M,PB⊥y轴于点B,交函数y=
(x>0)图象于点N.(点M、N不重合)
(1)当点P的横坐标为2时,求△PMN的面积;
(2)判断MN与BA的位置关系并说明理由;
(3)试问:△OMN能否为直角三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
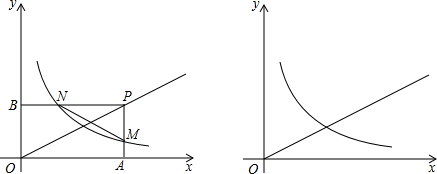
已知点P是函数y=
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
(1)当点P的横坐标为2时,求△PMN的面积;
(2)判断MN与BA的位置关系并说明理由;
(3)试问:△OMN能否为直角三角形?若能,请求出此时点P的坐标;若不能,请说明理由.

分析:(1)利用题中已知条件求出M和N的坐标,然后求出△PMN的面积;
(2)利用相似三角形,通过证明PM,PB和PN,PA相对成比例可证明△PAB∽△PMN.
(3)连接三个点,分别取三个点为顶点,求出不同情况下是否满足题目要求.
(2)利用相似三角形,通过证明PM,PB和PN,PA相对成比例可证明△PAB∽△PMN.
(3)连接三个点,分别取三个点为顶点,求出不同情况下是否满足题目要求.
解答:解:(1)∵点P是函数y=
x(x>0)图象上一个点,当点P的横坐标为2,
∴点P为(2,1),
由题意可得:M为(2,
),N为(1,1)
∴S△PMN=
×1×
=
;
(2)令点P为(2a,a),(a>0)
则A(2a,0),B(0,a),M(2a,
),N(
,a),
∴
=
=
,
=
=
,
即
=
∴MN∥AB;
 (3)由(2)得,ON2=a2+
(3)由(2)得,ON2=a2+
,OM2=4a2+
,
易知∠MON≠90°,
∴当∠ONM=90°时,
有4a2+
=a2+
+5a2-5+
,
解得a1=
,a2=
(舍去),即点P为(2
,
),
同理当∠OMN=90°时,点P为(
,
).
综上所述,当点P为(2
,
)或(
,
)时,能使△OMN为直角三角形.
| 1 |
| 2 |
∴点P为(2,1),
由题意可得:M为(2,
| 1 |
| 2 |
∴S△PMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)令点P为(2a,a),(a>0)
则A(2a,0),B(0,a),M(2a,
| 1 |
| 2a |
| 1 |
| a |
∴
| PA |
| PB |
| a |
| 2a |
| 1 |
| 2 |
| PM |
| PN |
a-
| ||
2a-
|
| 1 |
| 2 |
即
| PA |
| PB |
| PM |
| PN |
∴MN∥AB;
 (3)由(2)得,ON2=a2+
(3)由(2)得,ON2=a2+| 1 |
| a2 |
| 1 |
| 4a2 |
易知∠MON≠90°,
∴当∠ONM=90°时,
有4a2+
| 1 |
| 4a2 |
| 1 |
| a2 |
| 5 |
| 4a2 |
解得a1=
| 2 |
| ||
| 2 |
| 2 |
| 2 |
同理当∠OMN=90°时,点P为(
| ||
| 2 |
| ||
| 4 |
综上所述,当点P为(2
| 2 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握相似三角形性质以及用分类讨论解题的思路,此题难度较大.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
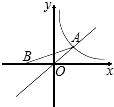 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=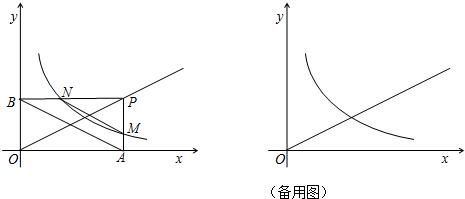
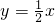 (x>0)图象上一点,PA⊥x轴于点A,交函数
(x>0)图象上一点,PA⊥x轴于点A,交函数 (x>0)图象于点M,PB⊥y轴于点B,交函数
(x>0)图象于点M,PB⊥y轴于点B,交函数