Question

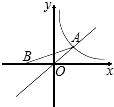如图，已知点A是函数y=x与y=

4

x

的图象在第一象限内的交点，点B在x轴负半轴上，且OA=OB，则△AOB的面积为（　　）

• A、2
• B、

  2

• C、2

  2

• D、4

Answer 1

分析：本题可以先求出A点坐标，再由OA=OB求出B点坐标，则S_△AOB=

1

2

|x_B||y_A|即可求出．

解答：解：点A是函数y=x与y=

4

x

的图象在第一象限内的交点，
则x=

4

x

，x=2，A（2，2），
又∵OA=OB=2

2

，
∴B（-2

2

，0），
则S_△AOB=

1

2

|x_B||y_A|=

1

2

×2

2

×2=2

2

．
故选C．

点评：本题考查了由函数图象求交点坐标，并求点之间连线所围成图形的面积的方法．