题目内容
10.如图,AB∥CD,∠AEC=90°(1)当CE平分∠ACD时,求证:AE平分∠BAC;
(2)移动直角顶点E点,如图,∠MCE=∠ECD,当E点转动时,问∠BAE与∠MCG是否存在确定的数量关系,并证明.(提示:可以作∠MCG的平分线)
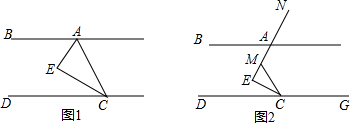
分析 (1)先根据平行线的性质得出∠BAE+∠CAE+∠DCE+∠ACE=180°,再由∠AEC=90°可知∠CAE+∠ACE=90°,故可得出∠BAE+∠DCE=90°,由CE平分∠ACD可知∠DCE=∠ACE,故∠ACE+∠BAE=90°,由此可得出结论;
(2)延长AE交DG于点F,根据平行线的性质可得出∠BAE=∠AFC,由∠AEC=90°可知∠CEF=90°,故可得出∠AFC+∠ECD=90°,再根据∠MCE=∠ECD,MCE+∠ECD=180°-∠MCG可得出结论.
解答 (1)证明:∵AB∥CD,
∴∠BAE+∠CAE+∠DCE+∠ACE=180°.
∵∠AEC=90°,
∴∠CAE+∠ACE=90°,
∴∠BAE+∠DCE=90°.
∵CE平分∠ACD,
∴∠DCE=∠ACE,
∴∠ACE+∠BAE=90°,
∴∠BAE=∠CAE,即AE平分∠BAC;
(2)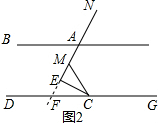 ∠BAE=$\frac{1}{2}$∠MCG.
∠BAE=$\frac{1}{2}$∠MCG.
证明:∵延长AE交DG于点F,
∵AB∥CD,
∴∠BAE=∠AFC.
∵∠AEC=90°,
∴∠CEF=90°,
∴∠AFC+∠ECD=90°.
∵∠MCE=∠ECD,MCE+∠ECD=180°-∠MCG,
∴∠BAE+$\frac{1}{2}$(180°-∠MCG)=90°,即∠BAE=$\frac{1}{2}$∠MCG.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
1.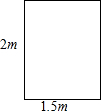 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
| A. | ①号 | B. | ②号 | C. | ③号 | D. | 均不能通过 |
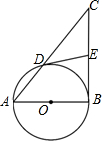 如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.
如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.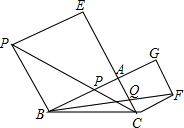 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.