题目内容
如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,且∠OBC=45°,则下列各式成立的是( )
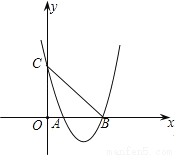
A.b﹣c﹣1=0 B.b+c﹣1=0 C.b﹣c+1=0 D.b+c+1=0
D 【解析】 试题分析:根据∠OBC=45°,有OB=OC,可设点C,B的坐标为(0,c),(c,0),把点B(c,0)代入二次函数y=x2+bx+c,得c2+bc+c=0,从而求出关系式. 【解析】 ∵∠OBC=45°, ∴OB=OC, ∴点C,B的坐标为(0,c),(c,0); 把点B(c,0)代入二次函数y=x2+bx+c,得c2+bc+c=0, ...
练习册系列答案
相关题目


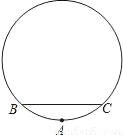
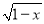 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )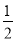 )﹣2+
)﹣2+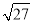 .
.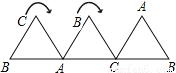
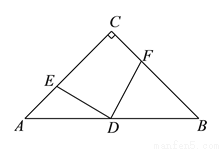
 中,
中, 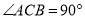 ,
, 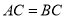 ,
, 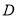 是
是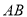 的中点,点
的中点,点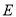 在
在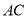 上,点
上,点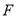 在
在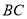 上,且
上,且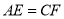 .
.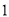 )求证:
)求证: 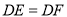 ,
, 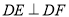 .
.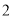 )若
)若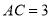 ,求四边形
,求四边形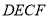 面积.
面积.