题目内容
2.当m,n是实数且满足m-n=mn时,就称点Q(m,$\frac{m}{n}$)为“奇异点”,已知点A是“奇异点”且在反比例函数y=$\frac{2}{x}$的图象上,则点A坐标为(1,2)或(-2,-1).分析 右已知条件得到$\frac{m}{n}$-1=m,即$\frac{m}{n}$=m+1,求得A(m,m+1),得到m(m+1)=2,解方程即可得到结论.
解答 解:∵m-n=mn且m,n是正实数,
∴$\frac{m}{n}$-1=m,即$\frac{m}{n}$=m+1,
∴A(m,m+1),
∴m(m+1)=2,
∴m=1,或m=-2,
∴A点的 坐标为(1,2)或(-2,-1),
故答案为:(1,2)或(-2,-1).
点评 本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的符合函数的解析式.

练习册系列答案
相关题目
13. 如图,四边形ABCD为⊙O的内接四边形,已知∠AOC=100°,则∠ADC的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠AOC=100°,则∠ADC的度数为( )
 如图,四边形ABCD为⊙O的内接四边形,已知∠AOC=100°,则∠ADC的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠AOC=100°,则∠ADC的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
13.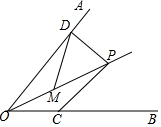 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 1cm |
11. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
12.在数-3,-2,0,3中,大小在-1和2之间的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 3 |