题目内容
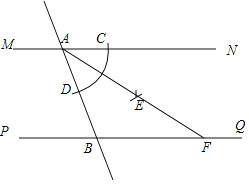
【题目】如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用以下步骤作图：
①以点A为圆心，适当长为半径作弧交射线AN于点C，交线段AB于点D；
②以点C为圆心，适当长为半径画弧；然后再以点D为圆心，同样长为半径画弧．前后两弧在∠NAB内交于点E；
③作射线AE，交PQ于点F；
若AF＝2
，∠FAN＝30°，则线段BF的长为_____．
【答案】2
【解析】
过B作BG⊥AF于G，依据AB=BF，运用等腰三角形的性质，即可得出GF的长，进而得到BF的长．
解：如图，过B作BG⊥AF于G，
∵MN∥PQ，
∴∠FAN＝∠3＝30°，
由题意得：AF平分∠NAB，
∴∠1＝∠2＝30°，
∴∠1＝∠3＝30°，
∴AB＝BF，
又∵BG⊥AF，
∴AG＝GF＝
AF＝
，
∴Rt△BFG中，BF＝
，
故答案为：2．
练习册系列答案
相关题目
