题目内容
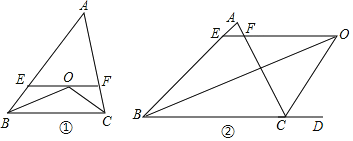
【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,请直接写出EF、BE、CF之间的关系 .
【答案】(1)EF=BE+CF,理由见解析;(2)EF=BE﹣CF,理由见解析
【解析】
(1)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系;
(2)等腰三角形有△BEO和△CFO,根据角平分线性质和平行线性质推出∠EBO=∠EOB,∠FOC=∠FCO,根据等角对等边推出即可;根据BE=OE,CF=OF即可得出EF与BE、CF之间的关系.
(1)EF=BE+CF,
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF;
(2)不成立,
理由:∵BO平分∠ABC,CO平分∠ACG,
∴∠EBO=∠OBC,∠FCO=∠OCG,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCG,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE﹣OF=BE﹣CF.
故答案为EF=BE﹣CF.

练习册系列答案
相关题目







