题目内容
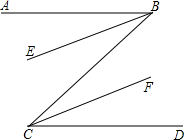 如图,如果∠ABC=60°,∠BCD=60°,BE,CF分别是∠ABC,∠BCD的平分线,那么BE与CF平行吗?
如图,如果∠ABC=60°,∠BCD=60°,BE,CF分别是∠ABC,∠BCD的平分线,那么BE与CF平行吗?
分析:观察图形可知,∠EBC和∠FCB是内错角,如果能说明这两个角相等,则可以得到BE∥CF.由平分线的定义易得∠EBC=∠FCB.
解答:解:BE与CF平行;
证明:∵∠ABC=60°,∠BCD=60°,BE,CF分别是∠ABC,∠BCD的平分线,
∴∠EBC=
∠ABC=30°,∠BCF=
∠BCD=30°,
∴∠EBC=∠FCB,
∴BE∥CF.(内错角相等,两直线平行)
证明:∵∠ABC=60°,∠BCD=60°,BE,CF分别是∠ABC,∠BCD的平分线,
∴∠EBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EBC=∠FCB,
∴BE∥CF.(内错角相等,两直线平行)
点评:本题主要考查平行线的判定,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 16、如图,如果△ABC≌△A′B′C′,那么∠A=
16、如图,如果△ABC≌△A′B′C′,那么∠A= 如图,如果△ABC中∠C是锐角,BC=a,AC=b.证明:S△ABC=
如图,如果△ABC中∠C是锐角,BC=a,AC=b.证明:S△ABC= 19、如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC=
19、如图,如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC= 如图,如果△ABC绕点O旋转90°后得到△DEF,且D与A是对应点,AD=4cm,则S△AOD=
如图,如果△ABC绕点O旋转90°后得到△DEF,且D与A是对应点,AD=4cm,则S△AOD= 如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论:
如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,对于以下结论: