Question

【题目】如图，直线与轴交于点，与轴交于点，抛物线经过、两点．

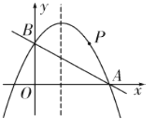
（1）求抛物线的解析式；

（2）若是抛物线上一点，且点坐标为，点为抛物线对称轴上一点，求的最小值；

（3）点为直线上的动点，点为抛物线上的动点，当以点、、、为顶点的四边形是平行四边形时，求点的坐标．

Answer 1

【答案】（1）；（2）QP＋QA的最小值为；（3）满足条件的点M的坐标为或或．

【解析】

（1）先通过直线与轴交于点，与轴交于点计算出A、B点的坐标，再代入计算即可；

（2）根据对称性知A点关于抛物线对称轴的对称点是，连接PC，则QP＋QA的最小值就是PC，从而计算即可；

（3）根据平行四边形的性质分为以OB为边和对角线两种情况分类讨论计算．

（1）∵直线与x轴交于点A，与y轴交于点B

∴A（2，0），B（0，1）

∵抛物线y＝－x2＋bx＋c经过A、B两点

∴

∴

∴抛物线解析式为

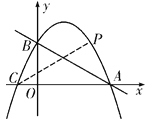
（2）如解图①，由（1）知，抛物线解析式为

∴抛物线的对称轴为直线，

抛物线与x轴的另一交点为

∵点A与点C关于对称轴对称

∴QP＋QA的最小值

就是

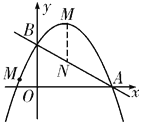
（3）①OB为平行四边形的边时，MN＝OB，MN∥OB

∵点N在直线AB上

∴设

∴

∴

Ⅰ．－m2＋2m＝1

解得，m＝1

∴

Ⅱ．－m2＋2m＝－1

解得，

∴或

②当OB为对角线时，OB与MN互相平分，交点为H，

∴OH＝BH，MH＝NH，

∵B（0，1），O（0，0），

∴，

设，，

∴，

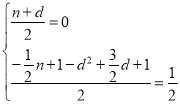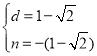∴或，

∴或；

即：满足条件的点M的坐标为或或．