题目内容
5．不等式组$\left\{\begin{array}{l}{2x+3＞1}\\{3x-6≤4}\end{array}\right.$的最大整数解为（ ）| A． | -1 | B． | -2 | C． | 1 | D． | 3 |
分析 先根据一元一次不等式组解出x的取值，然后找出最大整数解即可．
解答 解：$\left\{\begin{array}{l}{2x+3＞1①}\\{3x-6≤4②}\end{array}\right.$，
由①得，x＞-1，
由②得，x≤$\frac{10}{3}$，
则不等式组的解集为：-1＜x≤$\frac{10}{3}$，
故最大整数解为3．
故选D．
点评 此题考查的是一元一次不等式组的解法，根据x的取值范围，即可找出最大整数解．
练习册系列答案
相关题目
16．计算：（$\frac{1}{2}$）-1-（π-1）0，结果正确的是（ ）
| A． | 2 | B． | 1 | C． | -$\frac{1}{2}$ | D． | -$\frac{3}{2}$ |
20．国家统计局公布了2015年1月的居民消费价格指数（CPI），16个省市的CPI同比涨幅超过全国平均水平，其中7个省市的涨幅如表：
则这组数据的众数和中位数分别为（ ）
| 地区 | 北京 | 广东 | 上海 | 浙江 | 福建 | 云南 | 湖北 |
| 同比涨幅（%） | 3.3 | 3.3 | 3 | 2.8 | 2.8 | 2.8 | 2.3 |
| A． | 2.8，2.8 | B． | 2.8，2.9 | C． | 3.3，2.8 | D． | 2.8，3.0 |
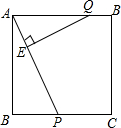如图，正方形ABCD的边长为3cm，P，Q分别从B，A出发沿BC，AD方向运动，P点的运动速度是1cm/秒，Q点的运动速度是2cm/秒，连接A，P并过Q作QE⊥AP垂足为E．