题目内容
15.一等腰三角形的两边长分别为2$\sqrt{5}$和3$\sqrt{2}$,其周长为4$\sqrt{5}$+3$\sqrt{2}$或2$\sqrt{5}$+6$\sqrt{2}$.分析 分两种情况:腰为2$\sqrt{5}$,底为3$\sqrt{2}$;底为2$\sqrt{5}$,腰为3$\sqrt{2}$;分别列式计算即可.
解答 解:当腰为2$\sqrt{5}$,底为3$\sqrt{2}$时,周长为2$\sqrt{5}$+2$\sqrt{5}$+3$\sqrt{2}$=4$\sqrt{5}$+3$\sqrt{2}$;
当底为2$\sqrt{5}$,腰为3$\sqrt{2}$时,周长为2$\sqrt{5}$+3$\sqrt{2}$+3$\sqrt{2}$=2$\sqrt{5}$+6$\sqrt{2}$.
故答案为:4$\sqrt{5}$+3$\sqrt{2}$或2$\sqrt{5}$+6$\sqrt{2}$.
点评 此题考查二次根式的实际运用,掌握等腰三角形的性质与三角形的三边关系是解决问题的关键.

练习册系列答案
相关题目
3. 如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
 如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.
如图,利用一面墙,用80米长的篱笆围成一个矩形场地,墙长为30m,围成鸡场的最大面积为( )平方米.| A. | 800 | B. | 750 | C. | 600 | D. | 2400 |
10.当1<a<2时,式子$\sqrt{(a-2)^{2}}$+|1-a|的值为( )
| A. | 3-2a | B. | 2a-3 | C. | -1 | D. | 1 |
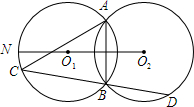 已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.
已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.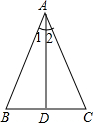 如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.
如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.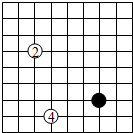 如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).
如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).