��Ŀ����
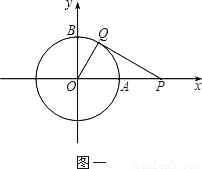
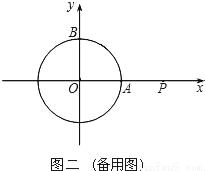
������ԭ��ΪԲ�ģ�1Ϊ�뾶��Բ�ֱ�x��y����������ڵ�A��B��
��1����ͼһ������P�ӵ�A����������x�����������˶������ͬʱ������Q�ӵ�B����������Բ�ܰ�˳ʱ�뷽�������˶�������Q���˶��ٶȱȵ�P���˶��ٶ���������1����P�˶����㣨2��0������ʱPQǡ���ǡ�O�����ߣ�����OQ�����QOP�Ĵ�С��
��2������Q���գ�1���еķ�����ٶȼ����˶�����Pͣ���ڵ㣨2��0�������������Q�پ���5���ֱ��PQ����O�صõ��ҳ���
��ϰ��ϵ�д�
�����Ŀ


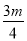 =0����������ȵ�ʵ������
=0����������ȵ�ʵ������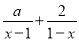 =1�Ľ��ǷǸ�������a��ȡֵ��Χ��_____��
=1�Ľ��ǷǸ�������a��ȡֵ��Χ��_____��