��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺�����C�İ뾶Ϊr����C��һ��P����C�����߳�С�ڻ����2r����ô��P������C�������ĵ���.
��1������O�İ뾶Ϊ1ʱ��
���ڵ�P1��![]() ��
�� ![]() ����P2��0����2����P3��
����P2��0����2����P3��![]() ��0���У���O�������ĵ����� ��
��0���У���O�������ĵ����� ��
�ڵ�P��m��n����ֱ��![]() �ϣ��ҵ�P�ǡ�O�������ĵ��������P������m��ȡֵ��Χ��
�ϣ��ҵ�P�ǡ�O�������ĵ��������P������m��ȡֵ��Χ��
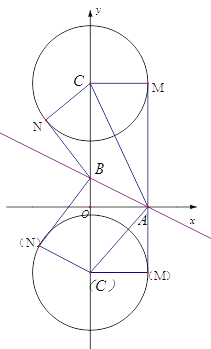
��2����C��Բ��C��y���ϣ��뾶Ϊ2��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B. ����߶�AB�ϵ����е㶼�ǡ�C�������ĵ�������ֱ��д��Բ��C�������ȡֵ��Χ.
��x�ᡢy��ֱ��ڵ�A��B. ����߶�AB�ϵ����е㶼�ǡ�C�������ĵ�������ֱ��д��Բ��C�������ȡֵ��Χ.
���𰸡���1����![]() ��
�� ![]() ����1��m��2����2��Բ��C������
����1��m��2����2��Բ��C������![]() ��ȡֵ��ΧΪ��
��ȡֵ��ΧΪ�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�������������������1����������㵽��O�����߳�������¶�������жϼ��ɵã�
���ú�m�Ĵ���ʽ��ʾ����P����O�����߳�������¶�����бȽϺ�õ�����m�IJ���ʽ�������ɵã�
��2�������A��B�������꣬��C����Ϊ��0��yC ����AM��BN�ֱ�Ϊ��C�����ߣ��е�ֱ�ΪM��N������AM2=![]() ��BN2 =
��BN2 =![]() �����߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱���ò���ʽ��
�����߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱���ò���ʽ��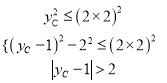 ���ⲻ��ʽ�鼴�ɵ�..
���ⲻ��ʽ�鼴�ɵ�..
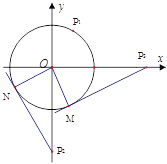
�����������1���ٹ���P2����O������P2N���е�ΪN������P3����O������P3M���е�ΪM��
���P2NO=��P3MO=90�㣬
��P2N=![]() =
=![]() ��
��
P3M=![]() =2��
=2��
�ߡ�O�İ뾶r=1�����P2��P3�ǡ�O�������ĵ�����
��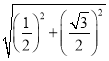 =1������P1��
=1������P1��![]() ��
�� ![]() ������O�ϣ����P1��
������O�ϣ����P1��![]() ��
�� ![]() ����ʾ��O�������ĵ�����
����ʾ��O�������ĵ�����
�ʴ�Ϊ�� ![]() ��
�� ![]() ��
��
�ڹ���P���ѵ�����PM���е�ΪM��
��P��m����m��3������PM2=PO2-OM2=m2+(-m+3)2-12=2m2-6m+8��
�ߵ�P�ǡ�O�������ĵ�������O�İ뾶Ϊ1��
��PM��2��
��2m2-6m+8�ܣ�2��1��2��
��1��m��2��
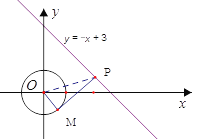
��2��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B������A��2��0����B��0��1����
��x�ᡢy��ֱ��ڵ�A��B������A��2��0����B��0��1����
��C����Ϊ��0��yC ����AM��BN�ֱ�Ϊ��C�����ߣ��е�ֱ�ΪM��N��
��ͼ��AM2=AC2-CM2=![]() =
=![]() ��
��
BN2=BC2-CN2=![]() ��
��
���߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱��
�� ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��Բ��C������![]() ��ȡֵ��ΧΪ��
��ȡֵ��ΧΪ�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.

 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д�����Ŀ��20��ײˣ���ÿ��18ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ��ǧ�ˣ� |
|
|
| 0 | 1 | 2.5 |
���� | 2 | 3 | 2 | 1 | 4 | 8 |
��1��20��ײ��У����ص�һ��������һ���� ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�1.3Ԫ���������20��ײ˿�������Ԫ��





