题目内容
14.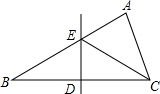 如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长?
如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长?
分析 根据线段垂直平分线性质得出BE=EC,BD=CD,根据△EDC的周长为24求出DE+BE+BD=24①,根据△ABC与四边形AEDC的周长之差为12求出BE+BD-DE=12②,两式相减即可求出答案.
解答 解:∵BC边上的垂直平分线DE交边BC于点D,交边AB于点E,
∴BE=EC,BD=CD,
∵△EDC的周长为24,
∴DE+EC+CD=24,
∴DE+BE+BD=24①,
∵△ABC与四边形AEDC的周长之差为12,
∴(AE+BE+BD+DC+AC)-(AE+DE+CD+AC)=12,
∴BE+BD-DE=12②,
∴①-②得:2DE=12,
∴DE=6.
点评 本题考查了线段垂直平分线性质的应用,能正确运用线段垂直平分线性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
5.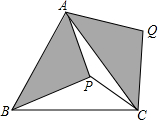 如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
 如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )| A. | 70° | B. | 80° | C. | 60° | D. | 50° |
2. 实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
 实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | a+c<0 | D. | b+c<0 |
19.两个相似三角形的最长边分别是35和14,它们的周长差是60,则大三角形的周长为( )
| A. | 80 | B. | 36 | C. | 40 | D. | 100 |
3.某数的$\frac{1}{5}$等于4与这个数的$\frac{4}{5}$的差,那么这个数是( )
| A. | 4 | B. | -4 | C. | 5 | D. | -5 |
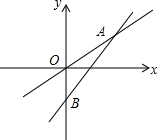 一个正比例函数与一个一次函数的图象如图所示,它们交于点A(4,3),一次函数的图象与y轴交于点B,且AO=2BO.求:
一个正比例函数与一个一次函数的图象如图所示,它们交于点A(4,3),一次函数的图象与y轴交于点B,且AO=2BO.求: