题目内容
如图,抛物线F: 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.
⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
解:(1) C(3,0);
(2)①抛物线 ,令
,令 =0,则
=0,则 =
= ,
,
∴A点坐标(0,c).
∵ ,∴
,∴  ,
,
∴点P的坐标为( ).
).
∵PD⊥ 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为( ).
).
根据题意,得a=a′,c= c′,∴抛物线F′的解析式为 .
.
又∵抛物线F′经过点D( ),∴
),∴ .
.
∴ .
.
又∵ ,∴
,∴ .
.
∴b:b′= .
.
②由①得,抛物线F′为 .
.
令y=0,则 .
.
∴ .
.
∵点D的横坐标为 ∴点C的坐标为(
∴点C的坐标为( ).
).
设直线OP的解析式为 .
.
∵点P的坐标为( ),
),
∴ ,∴
,∴ ,∴
,∴ .
.
∵点B是抛物线F与直线OP的交点,∴ .
.
∴ .
.
∵点P的横坐标为 ,∴点B的横坐标为
,∴点B的横坐标为 .
.
把 代入
代入 ,得
,得 .
.
∴点B的坐标为 .
.
∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
∴四边形OABC是平行四边形.
又∵∠AOC=90°,∴四边形OABC是矩形.
解析

练习册系列答案
相关题目
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.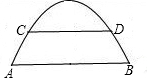 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4 ,水位上升3m,达到警戒线CD,这时水面宽
,水位上升3m,达到警戒线CD,这时水面宽 .若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
.若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.