题目内容
如图，已知，抛物线y=ax2+bx+c（a＜0）经过A（-1，0），C（0，1）两点，直线l与抛
物线相交于C，B（
，1）两点．
（1）求该抛物线的解析式；
（2）若点M（m，t）（m＜0，t＞0）在抛物线上，MN∥x轴，且与该抛物线的另一交点N，问：是否存在实数t，使得MN=2AO？若存在，求出t值，若不存在说明理由．
解：（1）当抛物线经过正点A，C，B时
解这个方程组得
所求抛物线的方程为y=
+
+1．
（2）若点m（m，t）在抛物线y=++1上，
设N（n，t），则有
+
+1=t，
又因为
+
+1=t，
故m，n是方程++1-t=0的两实数根；
∴m+n=，m•n=
（1-t）；
∴MN=n-m=
=2AO=2；
∴t=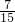
．
分析：（1）已知了A、B、C三点的解析式，代入抛物线中即可求得二次函数的解析式．
（2）由于MN与x轴平行，因此两点的纵坐标相等，设N点的坐标为（n，t）．将M、N的纵坐标代入抛物线的解析式中，可得出一个关于x的方程，那么m、n就是这个方程的两个实数根（可看做M、N是直线y=t与抛物线的两交点），可用m、n表示出MN的长，然后用一元二次方程根与系数的关系来求出t的值．
点评：考查一元二次方程的根与系数的关系，二次函数解析式的确定、函数图象交点等知识及综合应用知识、解决问题的能力．
解这个方程组得
所求抛物线的方程为y=
++1．（2）若点m（m，t）在抛物线y=
++1上，设N（n，t），则有
++1=t，又因为
++1=t，故m，n是方程
++1-t=0的两实数根；∴m+n=
，m•n=（1-t）；∴MN=n-m=
=2AO=2；∴t=
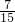．分析：（1）已知了A、B、C三点的解析式，代入抛物线中即可求得二次函数的解析式．
（2）由于MN与x轴平行，因此两点的纵坐标相等，设N点的坐标为（n，t）．将M、N的纵坐标代入抛物线的解析式中，可得出一个关于x的方程，那么m、n就是这个方程的两个实数根（可看做M、N是直线y=t与抛物线的两交点），可用m、n表示出MN的长，然后用一元二次方程根与系数的关系来求出t的值．
点评：考查一元二次方程的根与系数的关系，二次函数解析式的确定、函数图象交点等知识及综合应用知识、解决问题的能力．
练习册系列答案
备战中考寒假系列答案
相关题目
，且OA⊥AB，∠COB=45°．
如图，已知：抛物线y1=x2-2mx+1，y2=-x2-2mx-1，CE、DF分别是抛物线y1、y2的对称轴．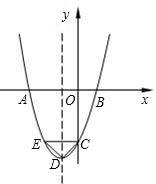
需写出解题步骤）．
（2011•利川市一模）如图，已知：抛物线y=ax2+bx-4（a≠0）与x轴交于A、B两点，与y轴交于点C，A、B两点的坐标分别为A（-6，0）、B（2，0）．